From RocketSlinger@SBCGlobal.net (email me there please)… This is a sub-site to main site at www.rocketslinger.com …

This web page last updated 11 Jan 2020

High-“G”-Force Impact-Landings Methods of Cargo Delivery to Earth’s Moon (or Other Heavenly Bodies Lacking an Atmosphere)

Abstract / Pre-Summary

This sub-page to www.rocketslinger.com is meant to describe methods of landing cargo on the moon, where the cargo is designed to withstand high “G” forces on an impact-type landing. Calculations are shown for considering different impact velocities, and different magnitudes (which are assumed to be uniform over elapsed time as a simplification) of the decelerating “G” forces. Thus, total deceleration time, and deceleration distance (the size of the decelerating mechanism) can be derived.

The incoming cargo vessel is assumed to come in for a hard landing on the moon, at a very low angle (at what could be called a tangent to the curvature of the moon’s spherical body). But before actual impact, the vessel could be pre-decelerated by throwing an “artificial atmosphere” into its path, at low altitudes. Most affordably and practically, such an “artificial atmosphere” would consist of clouds of moon dust. This feature is optional, and is briefly described here.

The decelerating mechanism on the surface of the moon is described in two primary versions. In both versions, the initial landing spot is surrounded by electronic (and-or visual) homing beacons for guidance. It is oval-shaped with a distorted half-shell of a funnel at one end (walls that tighten, similar to a cattle chute funnel). Alternately, an entire 3-D funnel could be used. A highly desired feature (for softening the very first stages of impact) would be to fill the oval landing area with several feet or yards’ depth of moon dust. The next stage of the decelerating mechanism could simply be linear. This might be a curved-bottom “V” shaped, long trough (channel). The channel could be filled with moon dust to assist the deceleration process, and-or, “break sticks” could be periodically positioned horizontally, part-ways up the channel walls, to be broken (and replaced between use-cycles) by the incoming vessel. The second main option for the design of the main body of the decelerating mechanism could a circular track (think of the curved walls at high-speed turns on an ice toboggan race track). The circular decelerating race-track would be constructed on the inside walls of a suitably sized crater. “Break sticks” could be used for deceleration once again, except that in this version, they would be oriented more closely to vertically, at least at the initial, highest speeds.

The shape of the cargo vessel could be most any shape, but spherical and bullet-shaped are the options considered here. In both cases, they should be constructed of materials intended for being processed (recycled) on the moon. Thus, they should be built of materials that are scarce on the moon (especially carbon and metals other than aluminum and iron). The outer layers of the vessel should be constructed to be “semi-sacrificial”, meaning that we assume that much of these layers will be abraded away during deceleration. However, abraded fragments (of any significant size) are assumed to be gathered up, post-impact-landing, for recycling (materials) uses. The innermost core of the vessel is assumed to (usually) survive the impact-landing, intact. Contents will have to be designed to withstand high “G” forces, of course. Composition, construction, and contents of the vessel are described in some detail here.

Almost as an afterthought, consideration here is also given to modifying the methods here described, to allow carrying humans, and other living things, in such a decelerating mechanism. “G” forces would have to be greatly lowered, and the “runway” greatly lengthened. Mathematics is used here (along with various speculative designs) to show that, at 3 G of deceleration, the decelerator or “runway” would have to be 27.3 miles long, and in other ways, impractical. Even if, as a costs-savings, the decelerator is suspended on cables (on towers instead of on the moon’s surface), this idea is judged to be too expensive. However, if technologies (especially materials science and engineering) become quite significantly more advanced than they are today, some of these ideas may become practical. Therefore, they are included here.

As with other sub-pages of www.rocketslinger.com , the intent here is to “defensively publish” propulsion-related (and “misc.”) ideas, to make them available to everyone “for free”, and to prevent “patent trolling” of (mostly) simple, basic ideas.

Introduction / “Why”

WHY should we want to spend resources to create a custom-built mechanism, on the moon’s surface, for high-speed (high-“G” forces) deceleration of cargo? Simply put, for fuel savings! We can save the bulk of the fuel that is spent on a lander-stage of a moon lander. Just look at the size of the Apollo landing stage (rocket engine, fuel, landing legs, etc.) compared to the payload section (the ascent stage)! Most of the mass of the landing stage can be eliminated, given only that the cargo is designed to withstand high “G” forces, and that the resources are invested, that are needed to build the decelerating mechanism. The “Blue Origin” lander (“Blue Moon”) shows the same large cost (large size of lander) v/s payload. See https://astronomy.com/news/2019/05/bezos-unveils-bold-plans-for-human-spaceflight-plus-a-blue-moon-lander , for example images.

Parenthetic note: I saw an article that claimed that, for lack of an atmosphere on the Moon (for use in aero braking and-or parachutes etc.), as an incoming SpaceX “Starship” lands on the Moon as opposed to Mars, the Starship will have to burn FAR more fuel to land on the Moon, than on Mars. So, despite the Moon’s lower gravity compared to Mars, the Starship can deliver only 12 tons of cargo to the Moon’s surface, v/s 100 tons to Mars’ surface. I can NOT re-find a link supporting this (slightly speculative?) “fact”, despite looking for it a long time! If you (reader) find it, please email me at RocketSlinger@SBCGlobal.net .

Basic Starting Facts, and Doing the Math

What sort of cargo would be targeted for delivering to the moon, using this kind of method as described here? One consideration is, what magnitude of “G” forces are we going to target, and what kinds of cargo can be selected or designed, that will withstand such forces? Consulting https://en.wikipedia.org/wiki/G-force , we now duplicate a few entries from their table, just for general illustration and for brief discussion:

Space Shuttle, maximum during launch and reentry 3 g

Maximum g-force in Tor missile system^[28] 30 g

Space gun with a barrel length of 1 km and a muzzle velocity of 6 km/s, as proposed by https://en.wikipedia.org/wiki/Quicklaunch (assuming constant acceleration) . . . . . . . . . . . . . . . . . . . . 1,800 g

Shock capability of mechanical wrist watches^[30][31] > 5,000 g

Rating of electronics built into military artillery shells^[34] 15,500 g

A sneak look-ahead peek (or two) from below, then, is that our calculations will guide us to targeting 50 to 100 “Gees” for our first-pass decelerators (not too large or expensive). For the further-distant future, human-safe decelerators (excluding very-very physically fit humans such as fighter pilots that might pull 8 or 9 “Gees”) should target pulling no more than 3 Gees, then, as above. But the above table out-takes CLEARLY show that many electronics, mechanical devices, and tools should easily be able to be designed (and packed) to withstand 100 Gees (and higher). Such higher-value items should be encapsulated (for maximum protection) at the very center of the cargo vessel. The same is true for gasses (to be discussed in more details later), as contained in sturdy-built COPVs (Carbon Over-Wrapped Pressure Vessels), or other strong storage tanks.

Besides the obvious cases of manufactured goods, what all kinds of raw materials might we want to ship to the moon, using this method? To select these materials, we need to know what materials are commonly available on the moon. Details about what kind of concentrations of what kinds of exploitable ores are located where, on the moon, aren’t yet available, for the most part. We already know that the moon’s north and south poles contain water-ice, in permanently shaded “cold traps” in the middles of craters. What we do NOT yet know, is what percentage of the captured volatiles there are NOT water, and what these volatiles are. Methane, ammonia, carbon dioxide, nitrogen, carbon monoxide, and-or others? I think that is fairly safe to assume that most of it is made of water.

What is the moon made of, at least at the accessible surface? https://www.thoughtco.com/what-is-the-moon-made-of-604005 says:

“The crust consists of 43% oxygen, 20% silicon, 19% magnesium, 10% iron, 3% calcium, 3% aluminum, and trace amounts of other elements…”

Accordingly, the very earliest bulk-materials cargos delivered by high-Gees “impact deliveries” might include partially processed (sheet metal, rolled metal, drawn wire, or ingots) of magnesium, iron (steel), and aluminum. SOME of such materials will survive impact-landing undamaged; damaged goods can be gathered and recycled. Metallic fragments will require less processing than raw ores! As time goes by, and native moon industries grow, such materials will be, more and more, be sourced locally. Later in time, bulk-cargo metals from Earth are likely to include copper, lead, zinc, titanium, tin, chromium, nickel, and zinc. More-precious elements (such as silver and gold) will be transported only at the well-protected innermost parts of the cargo vessel. The less-precious elements can be used to construct the outermost layers, where they can be (at least partially) abraded into small pieces (or torn away in large chunks), and gathered up out of the impact debris for use. Thus, at least SOME of the bulk materials will be lost… We’d not want to do that with silver or gold, or other precious metals!

Haphazard mixing of metallic elements thus delivered (and gathered from impact debris) would create extra troubles during sorting and use of such elements. So, the outermost layers of the first (say for instance) 10 or 15 vessels might be made of (say), copper. After that, the moon base has many years worth of copper supply “laid in”. All of the debris in and around the decelerator mechanism should then be thoroughly cleaned and sifted, recovering most of the copper. Then, the next (say) 8 or 12 vessels are titanium-clad. Thoroughly recover titanium debris, move to the next metal, rinse and repeat. These details will not be repeated below, and these parts (outermost abradable layers) of the vessel will often simply be referred to as “metal” (even though the metal will vary by exact type). Yes, some metals are too soft for decent structural use, and others are too brittle. Alloys and-or layering of different types of metal will often need to be used.

The other elements that will be needed as bulk cargo on the moon will include hydrogen and oxygen (only very early on; later on, water deposits should cover this), carbon, nitrogen, chlorine and fluorine (in fairly small amounts), and noble gasses (also in fairly small amounts). Some of these will most readily be delivered as pressurized and-or chilled gasses contained in COPVs (Carbon Over-Wrapped Pressure Vessels), or other strong storage tanks, located at the center of the vessel, for extra protection.

We can safely assume that large amounts of carbon will need to be delivered to the moon, for many years to come, if we’re serious about significantly-sized moon colonization efforts. Large amounts of carbon will be needed for (greenhouse) agriculture or advanced methods of food production, materials engineering / production, and for rocket fuel production. Note that Space X’s “Starship” runs on methane (CH₄), as an oxidant… Pure hydrogen is less practical for this (for use as an oxidant; it needs to be kept at lower temperatures than methane, even though burning hydrogen creates a higher-better “specific impulse” in rocket engines). For “Starship” (and similar) rockets to use the moon as a refueling station, using methane as the oxidant, carbon will have to be brought in to be combined with locally-sourced hydrogen (from water in “cold traps”). The moon has very-very little carbon… There are no shortcuts here.

Well OK, bringing in “carbonaceous chondrite” asteroids would be one possible “shortcut” here. However, bringing them in for use on the moon would benefit from the use of the exact same (or highly similar) deceleration methods as are described here (with some pre-processing of the asteroids’ constituent materials being highly desired; for example, to form them into the desired shape and size, at least roughly). Also, equip them with maneuvering cold-gas jets, so that they can hit their targets more precisely.

In what form do we bring in carbon? Carbon dioxide gas hardly makes sense, certainly not in the long term, because the oxygen part of this gas is already readily available on the moon, tied up in water (at the poles) and metal and silicon oxides (everywhere). So… Coal? Oil? Tar? Propane? Graphite? Charcoal? Structural plastics, PVC, epoxy, graphite, graphene, nanomaterials, or other carbon-containing structural materials composing parts of the vessel? Diamond (or even lonsdaleite) would be nice, but is obviously too expensive! All of these are possibilities. More details will be considered later. See https://en.wikipedia.org/wiki/Carbon and https://www.chemicool.com/elements/carbon.html for interesting (and relevant) facts about carbon. For now, consider this: Pure carbon turns into a gas at a temperature of 5,530 °C or 9,980 °F. Our impact-landing on the moon will create a lot of frictional heating. So, if the form of our carbon (we exclude diamond here for obvious reasons) is relatively pure carbon, very little of it will heat enough to gasify (and be lost to us, escaping in the non-existent “atmosphere” of the moon). Other forms of carbon (chemical compounds containing much oxygen or hydrogen, for example) will form complex gasses (including what we could simply call “smoke”) at much-much lower temperatures, and be lost to us, if frictionally heated on the moon’s surface. So we want to stick to more-pure carbon for bulk cargo, especially on the outer (abradable) layers of the cargo vessels (as contained in “pockets”; details further below). Candidates then are graphite (pure or near-pure carbon), charcoal (50% to 95% carbon, see http://www.fao.org/3/x5328e/x5328e0b.htm , typically around 70% to 80% carbon at the center of the distribution-shape bell curve), coal-charcoal or coal-“coke” (see https://en.wikipedia.org/wiki/Coke_(fuel), about 85% carbon for good-grade or steel-grade coke), petroleum coke (see https://en.wikipedia.org/wiki/Petroleum_coke, about 98.0% to 99.5% carbon for the pure grades), or anthracite coal (see https://geology.com/rocks/coal.shtml, about over 87% carbon). Incorporating such forms of carbon into the outer layers (“shells”) of a cargo vessel will be discussed in detail further below.

Now we move on to consider facts, and math, concerning velocities, “Gee” forces, and times and distances related to the deceleration process. See https://www.mpoweruk.com/Apollo_Moon_Shot.htm , where we see that 5,600 MPH was the incoming speed (in the Apollo program) of a spacecraft from Earth, in a “free return” orbit, without yet having burned the fuel required to perform “orbital insertion” into moon orbit. This will serve as our approximation of a good “high velocity” impact-landing. From the same source: After an orbital insertion burn for orbiting the moon at a low but stable altitude (of 69 miles), the orbital speed was 3,600 MPH. So this will serve as one lower-speed impact-landing, for calculations. Always recall: Lower impact speeds will shorten our runway, and – or lessen our “G” forces on impact, but will increase our rocket-fuel expenses (in slowing down before our “landing”) .

Almost parenthetically,

https://medium.com/teamindus/designing-a-propulsion-system-for-landing-on-the-moon-342878cf8067 is of general interest for landing profiles on the moon, using powered landings. If we used the (speed and elevation) numbers from there, we could clearly reduce the lengths of the “runways” that we will derive below. The price to be paid for that, though, would be more fuel (typically carried from Earth, at large expense), to slow down, first, for our “hard landing” on the moon. The 13 KM of elevation shown at the top of the graph is 13 KM * 0.621371 Miles / KM = a mere 8 miles of elevation (not 69), and 800 M/S of speed is 800 M/S * 0.000621371 Miles / M * 60 Min / Hour * 60 Secs / Min = 1,790 MPH (as opposed to the further-above figures of 5,600 and 3,600 MPH). This much-lower speed will be used from time to time, also, but always keeping in mind that the fuel savings will be much smaller.

Convert to feet per second for calculations… Back to miles when we estimate total “runway” (impact site for decelerations) length (distance travelled) when done with calculations…

High Speed: 5,600 MPH * 5,280 feet per miles * 1 hour / 3600 seconds = 8,213 feet / second initial “landing” speed

Medium Speed: 3,600 MPH * 5,280 feet per miles * 1 hour / 3600 seconds = 5,280 feet / second initial “landing” speed

Low Speed: 1,790 MPH * 5,280 feet per miles * 1 hour / 3600 seconds = 2,625 feet / second initial “landing” speed

For general comparison, the speed of a gun-bullet is about 2,500 feet / second.

Now see https://www-istp.gsfc.nasa.gov/stargaze/Sfall.htm where a slightly complex equation is given as Distance = t v _(mean) = ut + (1/2) gt² … However, VERY importantly, note that the situations (for us) are simpler than theirs, in that we have ONLY a starting speed, and a stopping speed that is ALWAYS zero. Note that we vastly simplify by assuming a uniform deceleration rate. The deceleration rate will depend on the coefficient of friction between the moon’s surface, and our impacting cargo vessel. Such friction will be very-very complex, and will need to be a matter of engineering experiments (iterative developments), to a large extent. These matters will be considered in much greater detail further below.

From the above link, note that v _{(mean) =} “…half the sum of the velocities at the start and at the finish”, which vastly reduces OUR particular complexity to merely… Distance = t v _(mean) = t * initial velocity / 2

Note, we are doing things in smaller steps for now; “t” (time in seconds) will have to be derived later, since it depends on “G” (Gee-force) of deceleration, which will help to determine our “Impact Landing runway Length”, which will thus be…

High Speed: 8,213 feet / second initial “landing” speed / 2 * “t” = distance; then distance = ( 8,213 ft/s / 2 ) * “t” = 4,106.5 feet / sec * “t” seconds

Medium Speed: 5,280 feet / second initial “landing” speed / 2 * “t” = distance; then distance = ( 5,280 ft/s / 2 ) * “t” = 2,640 feet / sec * “t” seconds

Low Speed: 2,625 feet / second initial “landing” speed / 2 * “t” = distance; then distance = ( 2,625 ft/s / 2 ) * “t” = 1,312.5 feet / sec * “t” seconds

“Baby steps” have now pre-digested our calculations for derived “t” travel time (in seconds) to decelerate to a dead stop, and for total distance (in feet).

See https://helmets.org/g.htm for a very succinct and well-written summary here, noting that Earth-normal “G” is defined as 32.2 ft / sec-squared, and that…

“at the start -- 0 (zero)
after 1 second-- g meters/second
after 2 seconds-- 2g meters/second
after 3 seconds-- 3g meters/second”

We are decelerating instead of accelerating, and we’re using feet, so for us… We will solve for “X” time in seconds…

at the time-start -- “initial” variable high-medium-slow speeds from above
after 1 second -- “initial” - 1g feet / second
after 2 seconds -- “initial” - 2g feet / second
after 3 seconds -- “initial” - 3g feet / second

after “X” seconds -- 0 (zero) feet / second = “initial” ft / sec – X sec * g feet / sec²

For purposes of units cancellation as a sanity check, we want to end up with “X” elapsed time in seconds. But keep in mind that the above shows feet /; sec (velocity), not feet / sec² (acceleration, as is usually attached to “g” figures), because the “seconds” in the denominator has been shifted to the left side of the equation. That is, only for 1, 2, and 3 seconds! At “X” seconds, we are back to “G” in feet / sec² (acceleration)!

The above is true, but confusingly stated. For those (probably vanishingly few) readers who REALLY want to follow all of this closely, with minimal opportunities for confusion, let’s modify the above block one more time, to show units details, for units cancellation sanity-checking, with “V” for velocity:

at the time-start -- “initial” variable high-medium-slow speeds from above
after 1 sec, “V” ft / sec = “initial” ft / sec – 1 sec * g ft / sec²
after 2 sec, “V” ft / sec = “initial” ft / sec – 2 sec * g ft / sec²
after 3 sec, “V” ft / sec = “initial” ft / sec – 3 sec * g ft / sec²

after “X” sec, “V” ft / sec = 0 (zero) ft / sec, so…

0 (zero) ft / sec = “initial” ft / sec – X sec * g feet / sec²

Modify the last bottom equation to create X sec * g feet / sec² = “initial” ft / sec (add the “X * g” term to both sides)… and finally X secs = ( “initial” ft / sec ) * ( 1 / g ( sec² / feet ) ) , and finally (re-stated) X secs = “initial” / g (numerically, skipping the units, as re-stated at the very end).

Paying attention to units cancellation above as a sanity check, we end up with “X” elapsed time in seconds, which is what we want. For having reached a dead stop, in our case.

Summary: So then generalizing for our situation, X seconds = init-speed / G, where “G” is our multiples of Earth-normal “g” of 32.2 ft / sec-squared. We have selected 3 G, 50 G, and 100 G for our numbers to play with. Multiply them out and we get (for us and our purposes)…

High G in ft/sec² = 3,200 ft / sec²

Medium G in ft/sec² = 1,600 ft / sec²

Low G in ft/sec² = 96.6 ft / sec²

Invert the above for ease of calculations and for ease of following the units cancelation and we get:

High G in sec²/ft = 0.0003125 sec² / ft ( 1 / G )

Medium G in sec²/ft = 0.000625 sec² / ft ( 1 / G )

Low G in sec²/ft = 0.01035 sec² / ft ( 1 / G )

Recall that for us, initially (at a time of “zero”):

High Speed: 8,213 feet / second initial “landing” speed

Medium Speed: 5,280 feet / second initial “landing” speed

Low Speed: 2,625 feet / second initial “landing” speed

(Baby steps all the way, keep in mind). Now derive our values of “t” in seconds, recalling that X secs = “initial” / g, or re-stated, X secs = “initial” * ( 1 / g ). :

High Speed High G: “t” = 8,213 feet / second * 0.0003125 sec² / ft

= 2.57 seconds

Medium Speed High G: “t” = 5,280 feet / second * 0.0003125 sec² / ft

= 1.65 seconds

Low Speed High G: “t” = 2,625 feet / second * 0.0003125 sec² / ft

= 0.820 seconds

High Speed Medium G: “t” = 8,213 feet / second * 0.000625 sec² / ft

= 5.133 seconds

Medium Speed Medium G: “t” = 5,280 feet / second * 0.000625 sec² / ft

= 3.300 seconds

Low Speed Medium G: “t” = 2,625 feet / second * 0.000625 sec² / ft

= 1.641 seconds

High Speed Low G: “t” = 8,213 feet / second * 0.01035 sec² / ft

= 85.00 seconds

Medium Speed Low G: “t” = 5,280 feet / second * 0.01035 sec² / ft

= 54.65 seconds

Low Speed Low G: “t” = 2,625 feet / second * 0.01035 sec² / ft

= 27.17 seconds

(Keep in mind that “Low G” here is “3”, selected for human passengers).

Now repeat the above, but de-cluttered, for summary purposes:

High Speed High G: “t” = 2.57 seconds

Medium Speed High G: “t” = 1.65 seconds

Low Speed High G: “t” = 0.820 seconds

High Speed Medium G: “t” = 5.133 seconds

Medium Speed Medium G: “t” = 3.300 seconds

Low Speed Medium G: “t” = 1.641 seconds

High Speed Low G: “t” = 85.00 seconds

Medium Speed Low G: “t” = 54.65 seconds

Low Speed Low G: “t” = 27.17 seconds

Recall from further above that mean velocities and time calculations (for total distance travelled derivations) will be distance = average speed times time, and will be (as shortened or summarized from above):

High Speed: 4,106.5 feet / sec * “t” seconds

Medium Speed: 2,640 feet / sec * “t” seconds

Low Speed: 1,312.5 feet / sec * “t” seconds

These calculations are so simple as to not deserve to be shown in great detail, any more. Run the numbers and you will get the below for “runway length”:

High Speed High G: “t” = 2.57 s, “d” = t * 4,106.5 ft/s = 10,554 feet

Medium Speed High G: “t” = 1.65 s, “d” = t * 2,640 ft/s = 4,356 feet

Low Speed High G: “t” = 0.820 s, “d” = t * 1,312.5 ft/s = 1,076 feet

High Speed Medium G: “t” = 5.133 s, “d” = t * 4,106.5 ft/s = 21,079 feet

Medium Speed Medium G: “t” = 3.300 s, “d” = t * 2,640 ft/s = 8,712 feet

Low Speed Medium G: “t” = 1.641 s, “d” = t * 1,312.5 ft/s = 2,154 feet

High Speed Low G: “t” = 85.00 s, “d” = t * 4,106.5 ft/s = 349,053 feet

Medium Speed Low G: “t” = 54.65 s, “d” = t * 2,640 ft/s = 144,276 feet

Low Speed Low G: “t” = 27.17 s, “d” = t * 1,312.5 ft/s = 35,661 feet

Repeat the above, de-cluttered and, for a better intuitive feel for how long (and practical or impractical) the “runway lengths” here might be, convert all the above to miles, with 5,280 feet per miles:

High Speed High G: “t” = 2.57 s, “d” 10,554 ft or 2.00 miles

Medium Speed High G: “t” = 1.65 s, “d” 4,356 ft or 0.83 miles

Low Speed High G: “t” = 0.820 s, “d” 1,076 ft or 0.20 miles

High Speed Medium G: “t” = 5.133 s, “d” 21,079 ft or 3.99 miles

Medium Speed Med G: “t” = 3.300 s, “d” 8,712 ft or 1.65 miles

Low Speed Medium G: “t” = 1.641 s, “d” 2,154 ft or 0.41 miles

High Speed Low G: “t” = 85.00 s, “d” 349,053 feet or 66.1 miles

Med Speed Low G: “t” = 54.65 s, “d” 144,276 feet or 27.3 miles

Low Speed Low G: “t” = 27.17 s, “d” 35,661 feet or 6.75 miles

The above should suffice to give us a rough idea of trade-offs in the numbers involved here, which will translate to economic and engineering practicality, as time and engineering developments progress.

Optionally Slowing Down Before Actual Impact

Note that some of what is to follow immediately below has been covered in http://www.rocketslinger.com/Ping_Pong_ME/ (same basic document is also at https://www.researchgate.net/publication/335218915_Ping_Pong_Mass_Momentum_and_Kinetic_Energy_Exchange_as_a_Method_of_Spacecraft_Propulsion ), as far as is concerned, slowing down our vessel before (in our cases here) it hits the deceleration mechanism. Moon dust is considered there (at http://www.rocketslinger.com/Ping_Pong_ME/ , especially in the sections centered around Figure #1 there) as a method of slowing down the vessel. Throw the moon dust into the path of the incoming vessel, and the moon dust will slow down the vessel. “ME bouncers” (Mass-Exchange, or kinetic-energy and momentum-energy exchange bouncers) are also described there. All of these methods would be compatible with what is being described here.

Before moving on, let us parenthetically add that, in the further-distant future, if significant construction activities ever take place on an “icy moon” further out in the solar system, finely powder ice, there, could take the place of “moon dust” as is here described, both for pre and post-impact slowing-down purposes.

At http://www.rocketslinger.com/Ping_Pong_ME/ (around Figure #1 there), mass accelerators (mass drivers, “space guns”) are considered for use, but the mathematics are not discussed. Let’s do that now, to see how practical (economical) such methods might be, for use here (for throwing up moon dust for deceleration).

From further up here, let’s repeat as below:

From https://en.wikipedia.org/wiki/G-force :

Space gun with a barrel length of 1 km and a muzzle velocity of 6 km/s, as proposed by https://en.wikipedia.org/wiki/Quicklaunch (assuming constant acceleration) . . . . . . . . . . . . . . . . . . . . 1,800 g

And also from https://en.wikipedia.org/wiki/G-force :

Standing on the Moon at its equator

0.1654 g

Now we have run these kinds of numbers before, so this time we can keep it shorter. We are going to put some numbers around the “moon dust clouds” as shown in Figure #1 at http://www.rocketslinger.com/Ping_Pong_ME/ … How big (long) would our “space gun” have to be, to put those dust clouds WAY up, 69 miles above the moon, where 69 miles is a low but stable orbital altitude as used during the Apollo era?

Let’s first see how far up above the moon we’d go with a “muzzle velocity” as given here, of 6 km/s. 6 km/s * 0.621 miles / km = 3.726 miles / sec;

3.726 miles / sec * 5,280 ft / mile = 19,637 ft / sec

Moon-gravity = 32.2 ft / sec² * 0.1654 = 5.33 ft / sec²

Our situation here is every bit as simple as what was described before… We have a starting-velocity and an ending-velocity of zero, so an average velocity of ½ of starting velocity, and travel time (as derived before) of X secs = “initial” / g… X secs = ( 19,637 ft / sec ) / (5.33 ft / sec² ) = 3,684 secs

Same as before, “d” distance traveled, as repeated from further above, is Distance = t v _(mean) = t * initial velocity / 2

Distance = 3,684 secs * ( 19,637 / 2 ) ft / sec = 36,171,354 feet!

36,171,354 feet * 1 mile / 5,280 feet = 6,851 miles

This is how high our purely-vertically-oriented “space gun” (of 1 km or 0.621 miles length) would be able to shoot our clouds of moon dust, straight up. We only need 69 miles up, to slow down our vessel (at low-stable orbit, Apollo style). Everything here is linear and proportional… There is no calculus involved here. So our “space gun” (for our needs at 69 miles) will be ( 69 / 6,851 ) * 0.621 miles = space-gun length of 0.006254 miles or 33 feet long. This may actually be possible, but expensive if many-many of them are needed, to loft up a significant amount of moon dust. The moon dust also clearly needs to be stretched out over time and distance, to smooth out the deceleration process, so many “space guns” will be needed. This may or may not be affordable, to loft up the moon dust very far (or “ME bouncers” as an alternative to moon dust, as described at http://www.rocketslinger.com/Ping_Pong_ME/ ).

So we may want to reserve these (optional) pre-slowing-down methods for lower altitudes, as we are coming in to our “hard landing”. Shooting for a MUCH lower altitude (not 69 miles) is ALSO desired, for allowing less time-of-travel to “spread out” our dust clouds too much (we want them to stay concentrated). Possibly more affordable are two methods described below (which were not mentioned at http://www.rocketslinger.com/Ping_Pong_ME/ ). We might limit ourselves to less-precisely-controlled (but more affordable), cruder methods of throwing up the moon dust, to only a few hundred feet vertically, at the most.

‘1) One or several centrifugal pumps. See https://en.wikipedia.org/wiki/Centrifugal_pump and – or https://www.michael-smith-engineers.co.uk/resources/useful-info/centrifugal-pumps . Such a pump could pump dust (particulate solids) every bit as much as it could pump liquids. Former farm boys (like me) will appreciate the similarity, here, to a silage chopper-and-lifter (centrifugal silage uploader), as is used to fill tall silos. The rotating element simultaneously chops up corn plants, and throws the resulting silage easily 100 feet up into the air, through a pipe, to fill a silo, over the top edge of the silo. A similar device (with a hopper-feeder full of moon dust) could loft moon dust into the path of the incoming vessel. Spin the device up ahead of time, using an electrical alternator (or motor), then open the hopper gate for feeding in moon dust, during the time the dust is actually needed. Guide the dust-stream as is needed by swiveling the shooter-pipe (or at least the end of the pipe) appropriately. Spin the rotational pump back down afterwards, recovering spin energy if desired.

Parenthetical notes; History buffs can use “Appleton silo filler” or “Ross silo filler” for search strings… Newer versions were made as well, but I can’t find them at a casual search-attempt. See https://www.flickr.com/photos/internetarchivebookimages/16642477306 for a sample image of an old-style silo filler or silage uploader.

‘2) Several gas (pneumatic) shooter-pistons (“air guns”). Fill a bottom chamber with pressurized gas (probably it’s best to use an inert but affordable gas like nitrogen or carbon dioxide). Gasses are expensive on the moon, so we want to conserve our gasses. One possible design is here described: The bottom chamber is fixed, and may or may not be cylindrical (this chamber has fixed walls). The top of the bottom chamber has a gas-outlet hole (gated by a solenoid or similar device) to explosively fill a shooter-piston cylindrical gas-expansion chamber. The gas-expansion chamber is topped off by a circular sliding member, which in turn is topped off by a cylindrical moon-dust-filled cylindrical chamber (gun barrel). The circular sliding member is NOT allowed to escape beyond the muzzle of the gun, so that gasses are retained.

At shooting time, the pressurized gas is explosively released into the gas-expansion chamber, shooting our moon dust out. After shooting time, the gas pump recovers the gas into the fixed, pressurized chamber, in preparation for the next operation. The sliding circular member can be tamped back down (from outside the device) when the moon dust chamber is re-filled, or it could be winched back down by a powered, internal mechanism.

Whether we use “space guns”, centrifugal pumps, or shooter-pistons (“air guns”), or some other method for shooting moon dust out (perhaps even gunpowder guns for example), we will have moving parts, and moon dust is harsh and abrasive! Whatever our shooter-devices will be, they will probably need frequent maintenance!

Also in any of the above-described cases, while en route to the moon, the incoming vessel could pre-deploy a parachute or parachute-like device, to catch more of the clouds of moon dust, for more efficiency. Figure #1 at http://www.rocketslinger.com/Ping_Pong_ME/ showed an inflatable device… That would work. A normal fabric parachute is probably NOT a good idea, because of the opening process! Such an opening process requires a real gas atmosphere, and opening time. An umbrella-like device (with spars) trailing behind the vessel sounds like an affordable but practical solution. The umbrella would require no gas fillings. A solid-metal parachute-like “dust catcher” could also work, trailing behind the cargo vessel. Such “dust catchers” (and their uses) will be described in more detail further below. Use “dust catcher” as a search string.

Entry to a Deceleration Device – The “Splash Pond”

The optional pre-deceleration process (using clouds of moon dust) has already been described. Next in the process (sequence) will be a “splash pond” full of moon dust, which will be almost mandatory, at least until such time that methods have been more fully developed. The splash pond will be oval-shaped, to cover imprecisions in the travel-path of the incoming vessel. It will be shallow at the edges, deeper in the middle, and filled with several feet or yards of moon dust. The bottom of the pond will (probably best) be smooth and hard. The bottom may be formed by micro-waving moon dust, for the final finish. See https://www.techbriefs.com/component/content/article/tb/techbriefs/physical-sciences/16856 for reference.

At the cargo-vessel-exit end of the oval splash pond, the incoming vessel (after shedding some speed in the “splash pond”) will be guided to a funnel or set of walls (think of a “V” shaped cattle chute) that will in turn guide the vessel to a linear or circular deceleration track. The “splash pond” will likely need to be re-filled with moon dust, or at least smoothed out, between uses. The splash pond scarcely deserves much more description, but will be shown in some of the drawings below. As usual, send comments / corrections / requests for clarification and – or drawings, to www.rocketslinger.com .

Construction of High-G-Impacting Cargo Vessels

The cargo vessel could be spherical (a ball), or a bullet shape, or anything else. A ball shape or a bullet shape will be the two shapes considered here. As previously mentioned, more-precious cargo will be secreted in the shielded center, while abradable outer layers will be made of bulk materials, such as pockets of fairly-pure versions of carbon (coal, graphite, charcoal, coke, etc.) and metal. These materials can be recovered as needed, from the impact debris. Let’s soon (below) discuss more details.

As far as the sizes of these vessels are concerned, generally, the bigger, the better! The larger the diameter, the greater the depth of the surface area (of the vessel) that can be abraded, before the more-precious innermost cargo is endangered. For the near-term future, we might envision a Space X “Starship” zipping around the moon in a free-return orbit, or performing an orbital-insertion burn. In either case, for cargo delivery, it wouldn’t need to land. While at the appropriate locations with respect to the moon, the Starship would release “whatever”… Small-sats, landers, and-or an impactor cargo vessel, and then return to Earth. ONE large cargo vessel, rather than many small ones, would usually make sense, for the above-described reason.

Space X Starship diameter (see https://en.wikipedia.org/wiki/SpaceX_Starship ) is about 30 feet ( 9 meters ). We’d need to spare some space around our enveloped cargo vessel, for Starship structural elements, plumbing, and wiring, and so our cargo vessel might be about 24, 25 feet or so in diameter. That will also show us, then, what the “radius of curvature” of the bottoms of the first versions of decelerator mechanisms might need to be. But for the rest of this document (including drawings), we will remain mostly agnostic concerning dimensions.

Before delving into more details about the construction and materials composition of the cargo vessels, let’s veer only a tiny bit off-topic, and consider the very earliest phases of the construction of a linear decelerator (the following comments are far-far less applicable, I think, to a curved or circular decelerator). We will want to carve a long trench into the moon’s surface. The lower the bottom of the trench is, the less time (and materials, labor, and money) we have to spend, building tall walls at the sides of the linear decelerator. So that sounds like a long, elongated impact crater to me! See https://en.wikipedia.org/wiki/Schiller_(crater) and https://www.abc.net.au/science/articles/2008/07/10/2299977.htm .

So, we could perform an almost military-style assault on the moon’s surface, in preparation for building a finished linear decelerator! We find a suitably located spot on the moon (close to a base, but not too close, to avoid danger). Already fairly flat and long (for a long “runway”). However, if other factors override us, and a few hills are in our way, we’ll blow them down! And we do almost definitely want to dig us a long, low trench.

So our first rounds of “high G impact cargo vessels” might not be much different than Earth-penetrating (moon-penetrating) bombs. See https://en.wikipedia.org/wiki/Bunker_buster . Moon-penetrating bombs might go a bit lighter on the explosives, and more heavily on the high-grade steel (plus maybe copper as well), than what has been used on Earth. This is because we are going dual-use here… After a few rounds of carving a trench and – or blowing away a hill, human-driven moon-moving gear, and – or robots, will go out to clear debris, AND fetch the impacted, scattered metals, for use on the moon. Clear the existing trench-bottom, that is, and prepare for the next round of cargo-bombs!

The following should be fairly obvious, but let’s state it for clarity and completeness: The cargo vessel will come in at a very-very low angle (a linear tangent to the curvature of the moon’s surface). Also, the cargo vessel (whatever its shape and size) will need to be equipped with guidance avionics and cold-gas thrusters (or even with maneuvering rockets and-or ion-based thrusters)… Whatever is needed to hit the target most accurately and affordably. The target will be identified by electronic and – or visual target markers. The controlled thrusters will control not only the initial impact target area, BUT ALSO the precise attitude (pitch, yaw, and roll) of the impacting vessel body, on first impact. This latter part is of special importance at least sometimes.

When the depth of hard rock that needs to be cleared away has become lessened, and only a shallow depth of rock needs to be cleared away (or at least shattered in order to facilitate removal), then we will need to move away from cargo-bombs, and towards “explosive armor clad” (or “reactive armor clad”) cargo vessels. See https://en.wikipedia.org/wiki/Reactive_armour . Here, the plan isn’t so much for the cargo vessel-bomb to PENETRATE the moon-rock, it is to KISS the moon-rock on a glancing blow, explosively blow up some moon rock, and then travel yet further down the trench, to inflict some more kinetic-energy-damage (and momentum-energy-damage) to further-distant stretches of the trench. If we have good attitude control of the incoming vessel, then only the vessel’s (bottom) skin areas that will touch the moon rock, will need to be clad with explosives.

Side benefits of carving a trench this way are at least two-fold, above and beyond delivering metals to the moon: ‘1) With remotely-located robotic seismographic stations scattered across the moon, these impacts should enable us to get a much better “view” of the guts of the moon (via differential travel-times of shock waves in different densities of rocks), and ‘2) the sides of the trench will enable geologists to view and sample deeper areas of the moon, which has not yet been done to much of any extent.

OK, so, then, some of our earliest cargo vessels will be cargo-bombs and reactive-armor-clad vessels. Enough of that, for now! Parenthetically, we might add, even after a far more “finished” linear decelerator is built, any impacting cargo-vessels that roll off of the end of the runway (or over-shoot, or both), will help (via impact energy) to carve a lengthened crude “runway” trench… For further construction refinement (finishing off) later.

Back, now, to primary materials (and construction details) for our cargo vessels, now that we have thoroughly covered the ideas around having some of the earliest ones being constructed to contain or incorporate explosives.

As mentioned (and listed) further above, we will want to build the vessels out of abradable outer layers of desired metals, and out of pockets of materials containing carbon, as one possible example of a construction method. Metals can be fastened to metals using the obvious methods of 3D printing, welding, brazing, solid castings, riveting, bolting, screwing, gluing, and so forth, and so, scarcely deserve any further mentioning. Fastening blocks of any form of carbon, into pocket inclusions, will deserve further discussion below.

As a starting drawing, here is a drawing of one bullet-shaped cargo vessel, with an almost-outermost layer (usually to be covered with yet another layer, with a final-outermost layer of mostly metal, excluding the “trimmings”, such as cold-gas maneuvering jets) of metal with carbon-containing inclusions.

Figure #1

Figure #1 (above) is simple and of low value, but it was easy to provide! It may provide SOME clarification to some readers, so here it is! The next drawing may fall into the same category, so here it is, also. It provides a closer-up and flattened-out view of an array of metal walls with enclosed pockets.

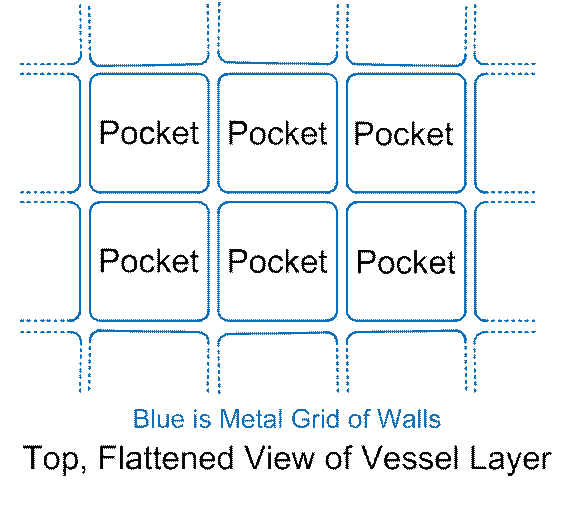
Figure #2

So now, we already have a number of variables that we can experimentally play with, to determine a high-level or gross “coefficient of friction” as we come in for a hard landing and a drawn-out deceleration process of the incoming vessel abrading its outer shells against a linear decelerator-trench’s walls. As time goes by and experimental data collects, we can deal with the composition of the trench-walls (to be addressed later), and the width, thickness, and composition of the vessel’s metal pocket-walls, as well as the more-solid metal layers between multiple pocket-containing metallic outer vessel layers. We can vary the contents from pocket to pocket, and the ratio of one or more kinds of pocket-contents to others. Graphite is a good solid-state lubricant, for example, so it might lessen friction between cargo vessel and trench-wall, as the vessel slides along (and the graphite is eroded away). Throw some graphite in some of these pockets then… And then maybe blocks of hard anthracite coal in other pockets, glued in, to resist abrasion and fragmentation, with “hard coal” being far more resistant than softer graphite, to increase the coefficient of friction. Play with the ratios of graphite pockets to anthracite pockets (and other types of pocket-contents, such as limestone, granite, or who knows what; some types of Earth-minerals would serve as good feed-stock for being finely ground up into the moon-dust during impact and vessel-wall erosion, to create “moon soil” for greenhouse agriculture on the moon, as the resulting debris is gathered and processed).

The contents of the pockets deserve more attention. For example, the pockets (at least some of them) could be filled with glued-together assorted sizes of balls of metals. As these pockets disintegrate during the impact-abrasion events, the balls of metals serve as “ball bearings” (at least, those that are not abraded into mangled shapes, as they are abraded out of the glue), as they will erode out of the glue and “pop out”, which (ball bearings) can then lubricate the sliding-along-the-trench motions of the remaining (aft segments of) cargo vessel. As is fairly well known (or certainly easy to grasp), circles (or spheres, as here) of different sizes can easily “nest into” one another, eliminating the need for much glue “fill” in our case. If we compose the different sizes of spheres (balls, ball bearings) out of different metal-types, in a consistent manner, then automated (or robotic) sorting mechanisms should easily be able to sort and recycle (recover) the different metals-types out of the impact debris, and out of the ground-down stubs of the incoming cargo vessels. This text (here) should be reasonably self-explanatory, but for ensured clarity, a drawing (an easy and simple one to draw) is provided below. The drawing is in two dimensions, but mentally extrapolating to three dimensions should be trivial. Think of beach balls, grapefruits, and marbles, for example.

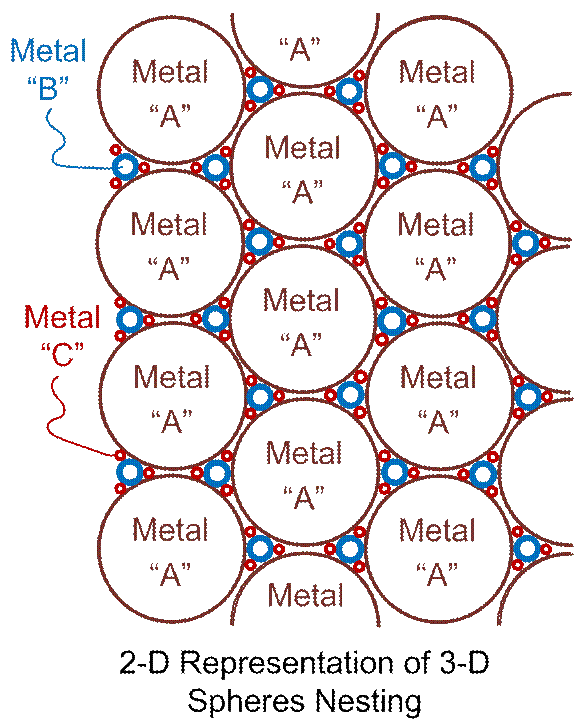
Figure #3

The “glue fill” between the nested spheres (“ball bearings”) of metal could be epoxy, petroleum tar, aerogel, poured Styrofoam, spray foam packaging material, or any other suitable fixating glue-fill (preferably containing decent amounts of carbon). The harder the fill, the higher the coefficient of friction (the harder for the ball bearings to roll / pop out of the cured glue, and perform a gross “lubricating” function on the incoming, remaining stub of the being-abraded cargo vessel). If the glue contains carbon, the carbon (and oxygen, hydrogen, and other volatiles) can be gathered and “baked out” of fragments large enough to be gathered and recycled. Depending on the glue compounds, some volatiles will be lost to frictional-heat-generated “smoke” upon impact, but so be it.

Variables to be experimented with, here, also include the number of “sandwich layers” of mostly-metal v/s metal with inclusion pockets. One might even be able to slowly roll a ball-form or bullet-form of cargo vessel with an inner layer of (encapsulated) precious cargo, a metal case, and then only ONE thick layer of mixed-spheres-and-glue, slowly cured as one rolls the vessels, and then only one final cladding-layer on the outside, of metal. More plausibly, center-peg the center assembly, and hold it in a spherical or cylindrical (bullet-shaped) mold, and pour the mix of balls and glue, around it. Or skip the inner, precious-cargo core, and just pour one large mold-full of glue-plus-balls. Cure it, pop it out of the mold, and metal-clad it. Or, mold and final outer case are one and the same. There are many possibilities available here…

Now suppose that our moon colonists find it difficult or expensive to sift ground-up carbon particles out of moon dust, in order to recover and use the carbon. They want lots of high-carbon bulk materials, but they don’t want to sift it out of moon dust after impact and abrasive deceleration. Graphite is fairly pure carbon, but it isn’t very hard. One possible solution here would be to encapsulate graphite inside ball-forms, egg-forms, or cylindrical (typically gelatin) pill-forms. Think of a child’s two-part plastic, hollow Easter eggs, or gelatin pill capsules. For us, the outer shells wouldn’t be made of plastic or gelatin; they would be made of fairly good-grade steel, or titanium, or other metal that will be useful on the moon. The two parts of the spheres (or egg-shapes or pill-shapes) would be secured to one another with threads on both parts, or glue, simple force-fitting, screws, bolts, or any other practical method. Just one tiny detail: One might usually want to leave a small hole as one end of your “Easter egg” for filling it with powder, after the two halves are joined. Plug the hole after the filling process is complete. Now throw your “Easter eggs” or “pills” into your mix of spheres-plus-glue. Some fraction of these will be shattered or abraded during the deceleration process, but many of them should survive, with their contents kept pure, for use on the moon.

Now, not only graphite, but other delicate solids and powders could be shipped this way, as well. Sugar, flour, chocolate powder, powdered milk, etc., could be shipped to your moon bakery, using this method! Or dried rice and beans for your moon survivalists, or “gorp” (trail mix) with dried fruits, nuts, and small candies. Beef jerky and fruit cakes. As teams of humans and robots sift through the impact debris and the abraded stub of the cargo vessels, looking for delectable treats, this will provide an entirely new meaning to an “Easter egg hunt”, as the humans find some yummy treats! Treats for robots? You will have to provide your own punch line here!

No seriously, shipping durable food goods this way should be quite plausible, so long as temperature extremes (especially on the high end) are avoided. Recover any post-impact food materials quickly, especially during hot moon “daylight hours”. Also note, in the Apollo program’s history, an inexpensive method of temperature regulation was used on the Apollo spacecraft, en route from Earth to the moon, and vice versa. If no preventive measures are taken (such as internal heat regulation methods), then the sunlit side of your spacecraft gets very hot, and the shaded side gets very cold. So the Apollo craft did a slow roll while travelling, for inexpensive temperature regulation. The Apollo astronauts called it the “rotisserie roll”. Space X or other “delivery vans” can do the same, to keep our durable-foods deliveries well preserved, en route.

What can be done with the contents of food-containing “Easter eggs” that get shattered or abraded, spilling their contents into the moon dust? Some “Half and Half”, for your coffee, anyone? “Half and Half” being half powdered milk, and half moon dust? But there’s no need to cry over spilled milk! Feed this mix into an industrial materials-recovery method, or dump it into your feedstock for deriving moon soil for moon greenhouses. Organic (carbon-containing) were-foodstuffs (foods damaged in any way) will feed your soil bacteria just fine.

Astronauts and moon colonists will have good senses of humor, without a doubt. Glue plus food-containing-Easter-eggs (spheroids and glue matrix) food deliveries will perhaps rapidly become known as “peanut brittle”!

More details about the construction of cargo vessels will follow, but they will be in the context of (and hence, listed with) individual types of decelerators.

A Linear Decelerator

The entrance to a linear decelerator might first consist of a “splash pond” full of moon dust, as was previously mentioned. At the exit end of the “splash pond”, there might be a funnel… A funnel, as is shown below. Or, the very top of the funnel might be lopped off (never built) as a cost savings, leaving a set of V-shaped walls (like a cattle chute), with the walls topped off with a bit of curled over-hangs, to help prevent a cargo vessel from spinning out of control, and “jumping the fence”. Some of this was described further above. The funnel and walls (as well as the pond-bottom) can be built out of mooncrete, with metal reinforcement where needed.

What was NOT described further above, will now be added: Reactive armor. Reactive armor (a cladding-layer of explosives) was mentioned further above, but in a different context. The top of our mooncrete funnel will be expensive, and hard to repair. So if we save money, by building the funnel to have an opening which does NOT exceed our way-worst-case but sometimes-probable “missing the target” scenario, then a cargo vessel might slam, occasionally, with great speed, into the upper lip of the funnel, which (funnel-lip) could easily be damaged, and be costly to repair. Such costs could VERY easily exceed the cost of a cargo vessel and unrecoverable contents. So we do MORE damage to any off-target vessel, and LESS damage to the upper funnel-lip, by using reactive armor, as shown in the cut-away cross-sectional drawing further below. In three dimensions, the reactive armor would be shaped like a distorted, downward-facing shovel-blade, covering perhaps about the top 1/4^th of the outermost lip, tapering off to a rounded-off finish (“cutting tip of the shovel blade)”, deeper in the tunnel-funnel.

Fairly obviously, a short and fat funnel (with a steep wall-angle meeting off-center-of-target incoming cargo vessels) will be less expensive, but impart higher “G” forces to an impacting off-center cargo vessel, as it is corrected-path-guided down the funnel. A longer funnel (with gentler angles on the walls) will perform better, but be more expensive to build. A hopefully-sensible “middle route” is diagrammed below.

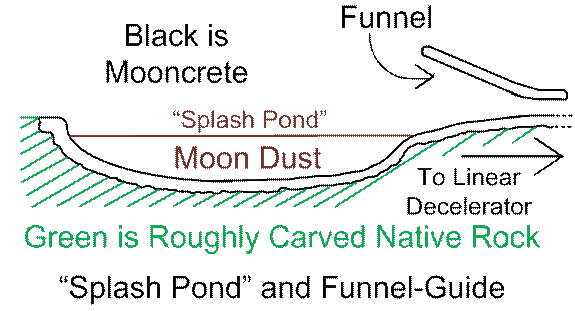
Figure #4

The above drawing is conceptual only… In reality, the “splash pond” would be longer, with a gentler entrance-edge on the left side above, and the moon-dust-fill would probably not be quite as deep as is shown.

Now, the next drawing will zoom in on the funnel, and show the “reactive armor”, as has been described further above.

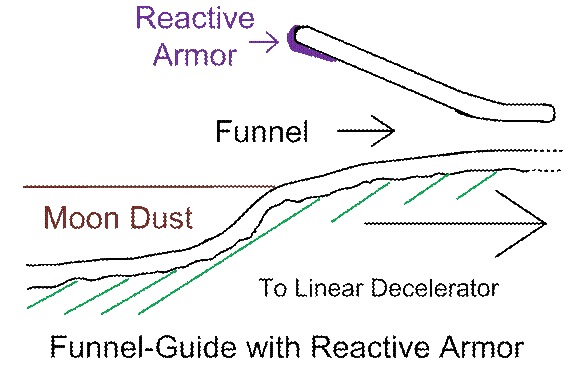
Figure #5

The above drawing, again, is conceptual only… In reality, some sort of cost-benefit analysis should be run on the exact desirable extent of the reactive armor. It might need to be applied on the roof of the funnel, deeper into the funnel… Or shallower, or not at all!

The long linear decelerator is a trough carved into the moon rock, perhaps at least partially initially carved by bombardment by low-angle-of-impact cargo vessels cum penetrator bombs and cargo vessels cum glancing-blow bombs, as described further above. Moon rock thus excavated can be piled onto the sides of the mooncrete as the trough is finished off (sides-reinforcing “backfill”). The top of the trough COULD be finished off with a roof (forming a tunnel), but that’s probably overkill, expenses-wise. The mooncrete bottom (of the trough) can be thin, since it is backed up by native moon rock. The walls of mooncrete will need to thicken up some more, where they are backed up only by broken-up backfill (rubble), and thicken up yet some more, probably, where they (the walls) are not backed up by anything. All this is true of the trough immediately following the entrance (funnel or input-guiding V-shaped walls; A funnel minus the top; AKA, a “cattle chute”). As the “bucking bronco”, AKA speeding sometimes-out-of-control, chaotic cargo vessel slows down, the strength of the walls can probably be reduced, further “downstream”.

At the tops of the walls, at least initially, to prevent an out-of-control cargo vessel from “jumping the fence”, we may want to provide a curved overhang of mooncrete. To save money, it might be hollow, or perhaps filled with a lower grade of mooncrete, with a higher percentage of moon rocks thrown in to reduce costs. These wall-tops should ideally be wide enough for wheeled vehicles to traverse, for purposes of trough maintenance and for gathering up impact debris, and the ground-down stubs of the cargo vessels.

More speculative (perhaps less plausible) ideas will be presented further below, but before providing the first drawing, let us describe one more set of ideas (which I consider to be most plausible): A linear decelerator should specialize in one of two major categories; Suitable for either spherical or bullet-shaped cargo vessels. Let’s first discuss and diagram the version built for spherical cargo vessels.

A spherical vessel (in the trough) will tend to roll, simply because it encounters friction at the bottom, but not the top. If the roll rate (spin rate) is high enough, it will damage internal cargo, or even cause the entire vessel to simply fall apart entirely, from centrifugal forces tearing it apart. A highly plausible (and practical) counter-measure here, is simply to balance the deceleration forces. At the bottom, we already have friction with the trough bottom. The finish or “paint job” there will be a way to adjust friction, but will not be further discussed here. At the TOP of the rolling cargo-vessel-ball, we can slot the trough-walls, and place “break sticks” in these wall-slots. The break sticks can be made of mooncrete, metal, plastic, plastic blended with moon dust, ceramics, or any suitable material that is easily sourced and-or recycled (3D printed?) on the moon. The spacing and strength of these “break sticks” will help adjust the gross “coefficient of friction” (and hence, of course, the deceleration rate). These sticks will counter-act the tendency for the ball-vessel to pick up a too-high spin rate as well. The slots in the trough-walls will need to be deep enough and strong enough (and probably metal-lined) in order to prevent the stick-breaking process from damaging the slots in the mooncrete walls.

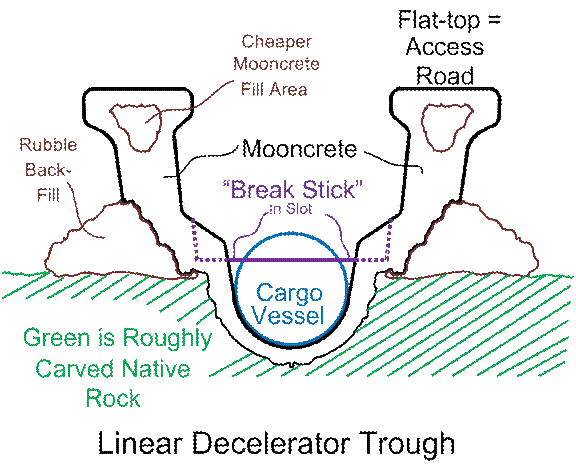
Figure #6

The above drawing and description (in my opinion) describe the most plausible design for a linear decelerator using a spherical cargo vessel, and it does NOT call for intentionally filling the trough with moon dust, as a method for providing or adjusting gross “friction”. That’s what the “break sticks” are for. These sticks will need to be replaced for each cargo delivery, which is a disadvantage. An advantage is that the trough can remain mostly empty of moon dust, meaning that abraded fragments of the cargo vessel will NOT have to be sifted or sorted out of moon dust.

Now let’s describe some associated ideas that I consider to be less plausible. Please don’t forget, my intentions here are to fend off the “patent trolls”, thus facilitating affordable future technology developments… Less-plausible ideas are fair game! Being less plausible, though, I provide no drawings for these ideas… If readers want more drawings, as usual, please email me at RocketSlinger@SBCGlobal.net .

The “break sticks” here MIGHT be able to be replaced by more durable restraints. Perhaps strung-together segments of straight elements alternating with rope, cable, chain, or large-rubber-band-like, stretchable material, and perhaps including small wheels spinning around the straight elements (with each straight element acting as a wheels-axis). These restraints might be spring-loaded, with the springs buried in the trough-wall-slots, so that they can stretch. Such restraints would need periodic inspection and maintenance, clearly, but they MIGHT be able to deflect up around the ball (vessel), and NOT need to be replaced for each cycle of use, while still providing “friction”. Tilting the wall-slots, so that the tops of the slots tilt away from the ball, should help. I am skeptical. Keep in mind that we have a VERY harsh environment on the moon, so such a design would have to be built ruggedly. AND, as has been previously remarked, the initial “landing speed” will literally be “faster than a speeding bullet”!

Another variation of the above might be called the “giant guitar picks” method. Higher up the trough-walls, place fairly strong cross-bars. Hanging down from these cross-bars (which reside above the expected path of the ball-vessel), are the “giant guitar picks”, which are stiff but flexible… With bottoms at least slightly tiled away from the ball. Wayward too-high balls will sometimes break your cross-bars, and the “guitar picks” will wear out, and degrade in the harsh environment. But maintenance costs MIGHT be lower than that of the “break sticks” method. “Guitar picks” might be made of plastic, or, probably far more durable, Fiberglass. They might best have a “C” shape, with the open end downwards, “cupping” the rolling ball, and with this open-bottom edge lined with hairs or bristles, with the hairs stiffening further up. This would still impede the rolling ball, while reducing abrasion, and hence, maintenance costs. “Guitar picks” would easily be damaged by bullet-like speeds of the cargo vessel, of course. Still, they are described (and diagrammed) in much greater detail, further below. Use search-string “guitar pick”.

If restraint mechanisms other than simple “break sticks” (to include “guitar picks”) are to be tried out, a good idea would be to start trying them in the lowest-stress environments first. That means working from the lowest-speed (speed of the cargo vessel in the decelerator) end, towards the “upstream” highest-speed end, as these hopefully-lower-maintenance methods are developed. Only some large advancements in materials science and engineering is likely to make these ideas plausible.

Other perhaps-less-plausible associated ideas here would include filling the trough with moon dust (and-or moon-sand or moon-gravel, or other matter to be “plowed through”). Moon dust suspended in aerogels, Styrofoam, or other solidified foam(s) are examples of other options. This method could apply to cargo vessels of any shape. In order to distribute the “friction” of plowing through this matter (and not have it applied to the vessel, only at the very bottom of the trench), one could top off the trench, and turn it into a tunnel. Then, the path-impeding matter could be dropped from the tunnel-roof at the precisely correct times. OR, the impeding matter could be thrown (puffed, blown) UP from the BOTTOM of the trench, at the precisely correct times. Air guns, explosive charges, rail guns, centrifugal pumps, or any other suitable method could be used. I am, again, skeptical concerning the practicality of such methods.

One final less-plausible (but not at all totally implausible) method brings us back to using the spherical cargo vessel, primarily, but adding “hair” to it. This might be especially useful at the phase of the journey where the cargo vessel hits the moon-dust-filled “splash pond”. A rebounding (bouncing) action here could be troublesome. Rolling will start to set in as well. A helpful countermeasure here could be to add “hair” to the ball. “Hair” here would likely be different, mixed lengths, thicknesses, and types of cable, chain, wire, and-or rope. If any rope is used, it would likely be wise to add at least SOME strands of metal to it, to facilitate using electromagnetic “metal detector” technology to fish fragments of abraded-off rope out of the moon dust. This “hair”, alone, should help the ball “stick to” the moon dust… Think of a large mop… And alleviate bouncing and rolling actions.

A highly probable improvement, exceeding the above, would be to add to the outermost tips of most or all of these “hairs”, dust-catchers. The dust-catchers could be of different sizes, adjusted per hair-size, and made of a hollow metal shell. These could be shaped like “Hershey’s Kisses” (also similar to the Apollo-style atmospheric-re-entry capsule or Command Module). At the small tip, there could be a loop, for tying to the “hair”. Then, add large holes (or slots) in the metal body, for dust inlets, roughly halfway down towards the flattened bottom of the “Hershey’s Kiss”. The bottom half (or so) is solid-walled and hollow, for catching and retaining moon dust (or other “impeding matter”). Any rolling action will now be strongly impeded, by centrifugal force throwing these dust-filled “Hershey’s Kisses” out to maximum radii as allowed by the “hairs” lengths. Rolling action will ALSO be impeded when the “Hershey’s Kisses” slam down into the dust (or walls or floors) on the leading edge of the ball-path.

Dust catchers as described here, could also, aptly, be considered to be small, metallic “parachutes” for collecting dust. They could also be used for helping to catch pre-landing, lofted dust clouds, as shown in Figure #1 at http://www.rocketslinger.com/Ping_Pong_ME/ .

This set of ideas could also be applied to a bullet-shaped cargo vessel. With this shape of vessel, the “rolling” problem of the ball (when hitting the “splash pond” full of moon dust, or other impeding matter, in a pond, or in a trough) becomes a “cartwheeling”, “somersaulting”, or a “porpoising” problem (as in an aircraft landing for the latter term). For the bullet shape, we really don’t need “hair” and dust-catchers all over the vessel body… We just need them trailing off of the aft end. Here, a visual analogy is to the tin cans tied to the aft end of the honeymooners’ car. The trailing hairs and dust-catchers will serve to help “peg” the relative position of the trailing end of the vessel, stabilizing its attitude during travel, and adding drag. These dust-catchers might therefor aptly be called “dust anchors”. In order to use such an arrangement optimally, on a bullet shape, not only should one try to hit the “splash pond” with the aft end of the bullet shape lower (attitude-control-wise) than the fore end, one might also wish to be slowly ROTATING (spinning) the arrangement of rear-facing “hairs” and dust-catchers, so that centrifugal force will fling the dust catchers out and away from the centerline of the vessel, catching dust even before the vessel-body touches the dust.

This idea may or may not be practical. It sounds like a fair amount of extra trouble to me. It is NOT totally implausible or impractical, though, in my opinion. But I highly doubt that it would be compatible with the idea of using “reactive armor” on the top lip of a funnel, as in figure #5. Dust catchers (whether or not they are still tied to the vessel) hitting the reactive armor is too great of a danger.

Next, let’s examine the issues (and possible solutions) involved with a linear decelerator and a bullet-shaped cargo vessel, as opposed to a spherical cargo vessel. As mentioned further above (in the context of a bullet shape entering the “splash pond” full of moon dust or other travel-impeding matter), “somersaulting” or tumbling (heels over head; aft end over fore end) can be a problem. Suppose we fill our linear decelerator trough (trench) with moon dust (or some such). If we have BOTH ends of the bullet shape throwing moon dust upwards, then the vectors thus created will tend to peg BOTH ends of the bullet-shape down into the trench, preventing tumbling. At the fore end of the bullet shape, carve the appropriate (probably best curved-shaped) carve-out as shown below. Along the bottom length of the majority of the vessel, remove more material from the bullet shape. At the aft end, leave a scoop, and an internal channel for throwing moon dust upwards, through the middle rear of the vessel.

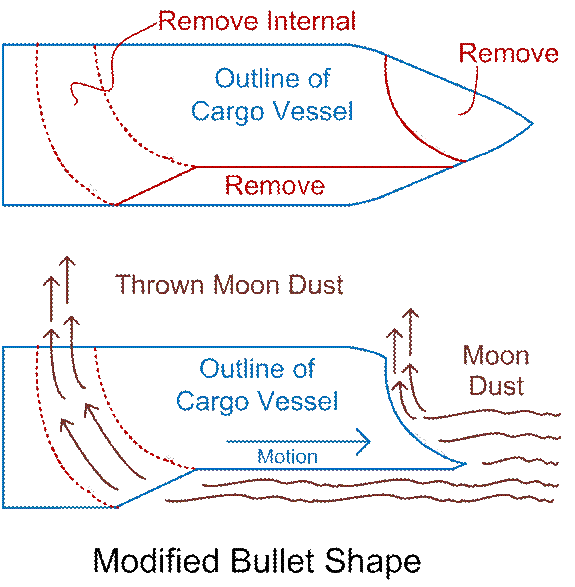
Figure #7

So the bullet-shaped vessel nestles into the bottom of the trough, and throws moon dust (out of the trough) upwards, to stabilize itself. Compared to a trough designed for a rolling ball (Figure #6), the trough here might best be wider, with shallower-angled walls, so as to re-catch most of the upwards-ejected moon dust, as the dust settles back down, to lessen maintenance costs. “Break sticks” (or other restraining devices) could thus be eliminated, although they could optionally still be used. A price to be paid for the use of the moon dust, is that now abraded-off segments of a cargo vessel do need to be sifted out of the moon dust, and the abraded-down stump of the vessel is now messier (dustier) as well.

One MIGHT be able to eliminate out of the design (or at least reduce in size), the “splash pond” and – or funnel, but (safely) ONLY if one has excellent control of the incoming path, as well as the incoming attitude of the cargo vessel, here. (The best approach attitude does include the aft end being located at least slightly lower than the fore end). If the attitude is wrong, the “snow-plow-like” moon-dust plows won’t work (for not being located at the bottom of the dust-filled trough).

The other problem (only now to be briefly discussed) is, the situation in figure #7 is nice and cozy, but how do we “land” (touch down), so as to get into this cozy position, in the first place? Search further above for “Hershey’s Kisses” or for “dust anchor”, and you will see part of the answer. Think also of the tail hook on an aircraft landing on an aircraft carrier. Here, we replace the tail hook with a bushy tail, a tail-mop, or a tail-mop with “dust anchors”, for a gentler initial landing, because of our high incoming speed. The scary possibility is that the tail-device will bounce, torqueing the bullet-body around its “center of mass”, driving the aft end of the bullet up, the fore end down, and initiating a tumble.

A good solution is to lengthen the tailhook-like device (make a large part of its length be “telescoping”). Now, the long lever arm increases the resistance towards initiating spin on the bullet-plus-tailhook (the spin inertia or angular momentum inertia of the entire body is increased). Forward inertia of the bullet, plus the drag of the tailhook device, combine vectors to settle the bullet (in a good attitude) into the dust.

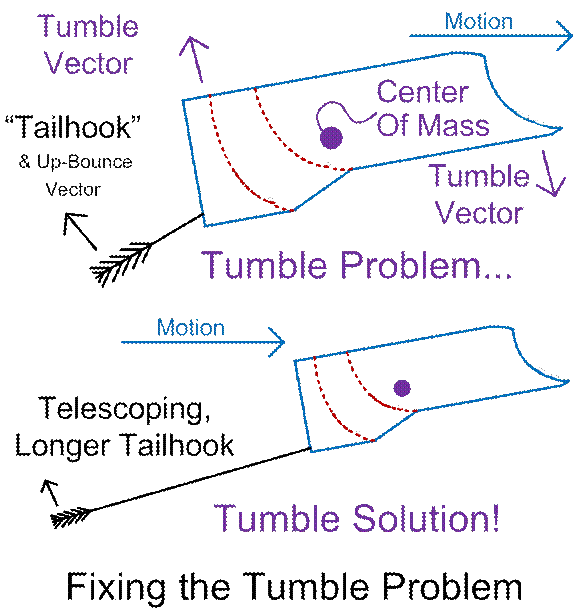
Figure #8

Keep on mind that we have previously stipulated that these cargo vessels are going to need to incorporate mechanisms for adjusting (fine-tuning) trajectory and attitude. These will most likely be cold-gas maneuvering jets. They can also be used for correcting tumbling (and “fishtailing”) problems as well, at first-impact time, and surrounding this time. However, reaction speeds of such maneuvering jets would need to be exorbitantly fast, for this purpose, and we wish to minimize the need for much propellant, as well. That’s actually the main motive for wanting to use moon-surface decelerators in the first place.

It would also be possible to add, spaced out over the outer surface of the bullet shape, recessed wheels that only protrude partially. As the vessel slows down, added resistive braking could be used. Such wheels could be used with or without moon dust. They’d obviously be seriously degraded by abrasive moon dust, but the cargo vessels here envisioned, are sacrificial anyway (are meant to be torn down for materials). If such wheels are included on ALL surfaces of the bullet shape, we wouldn’t even need to worry so much about the proper attitude of the bullet shape, as far as is concerned, which flank is “up” and which flank is “down”.

If wheels, and no moon dust, are used, the “snow-plow” shapes can, of course, be omitted. The tailhook can go to being a simple brush (no “Hershey’s Kisses” style “dust anchors” make sense any more). One could then add “break sticks” (or other restraining devices) into the design, as in Figure #6. In this case, the break sticks could be placed clearly ABOVE the body of the travelling bullet shape, to be used (broken) ONLY in case of “tumbling motion” starting in. In fact, two or more (vertically spaced) layers of “break sticks” could be added, with stronger ones located higher up, as safety measures against “tumbling”. In this latter scenario of “break stick” use, having the vessel hit a fairly precisely defined landing spot becomes more and more critical, in order to avoid a chaotic landing, while still benefitting from the “break sticks”.

A Curved Decelerator

The entrance to a curved decelerator will almost definitely require some sort of “splash pond”, funnel, and–or some length of linear decelerator, before entering into the curved decelerator. Either that, or we need absurdly high precision on hitting our target. A funnel entrance to the curved part could consist party (or largely or entirely) of a tunnel carved into the mountains (ejecta walls) surrounding a circular crater. As one excavates and processes the volatiles-containing materials in a permanently shaded crater, one will likely need rock-and-soil-moving equipment located there, for this effort, anyway. It might be very efficient to work inwards around the edges of the crater-fill material, moving the depleted materials towards the crater walls. As part of this effort, the depleted materials (or at least some of them) could be used to shape a curved decelerator, curving around the inside of the crater walls.

Adding more and more length to an existing linear decelerator is pretty trivial… One site-selects well for this (one doesn’t site said short decelerator terminating into a mountain side). For doing the same with a curved decelerator, for the option of later lengthening, one selects a crater that’s larger than initially needed. But then the curve-rate goes down, cutting back part of the benefit of a curved decelerator. That benefit is that centrifugal force can provide part of our “coefficient of friction”, as the ball rolls around. (Perhaps better stated, put it this way: At least at the initial high speeds, centrifugal force will push the vessel very strongly, into the curved path-bottom, helping to provide friction). No moon dust should be needed. “Break sticks” (or other restraining devices) come back into the picture, for preventing spin energies from going too high.

Getting back to site selection (crater-size selection), one could select a decent-sized (not too large) crater, and locate the initial entrance to the curve, perhaps a bit on the high side. Drop the curved path down over a gradient, so that, in the future, if desired, the path could drop down to overlap the existing path, one layer lower (and–or further inward, with a tighter radius), without any sharp angles in the path. Think of a spiraled snail shell here…

Other options are possible, here, but to me, only the ball-shaped (spherical) cargo vessel makes much sense for use in this context. “Break sticks” (or other restraining, anti-spin devices) come back into the picture, as previously mentioned, and the curved track (bobsled style or toboggan-racetrack-style) needs to be tilted up and outwards. The “break sticks” tilt up as well, approaching vertical, at least at the beginning of the track, with the tilt diminishing later (at lower speeds). A “roll out” apron or skirt is arrayed around the inner rim of the track, which eases the job of gathering abraded-off remnants of the vessel, as well as the abraded stub of the vessel. It is here called a “roll out” skirt, simply because a ball will “roll out” of the tilted path as soon as the centrifugal force is too low to pin the ball to the outer wall, any longer.

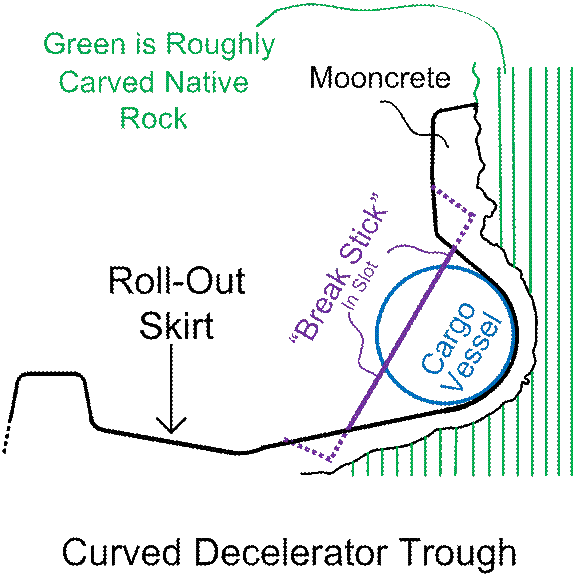
Figure #9

This concludes the descriptions of ideas that are far-more directed towards high-G-forces resistant cargo, than they are directed towards, first, bringing the G-forces WAY down, then proving reliability and safety, and THEN, possibly using such methods for bringing in passenger vessels.

Designs for Passenger-Rated Decelerators

The entire focus of this over-all document here shifts radically now. Keep in mind, as usually, the main purpose of this document is to fend off future “patent trolls”. Basic, fairly simple ideas are documented here… Sometimes they are plausible, and sometimes they aren’t. Some of today’s implausible ideas will become practical in the future, though, with new technologies, and especially with newer, better, yet still affordable materials.

This is a good time to briefly look over above results, give them a sober, frank assessment, run some more calculations, gather some more facts, and start a fresh “go” at all of this, with an eye towards eventually carrying passengers.

Repeated/modified from above:

High Speed: 8,213 feet / second initial “landing” speed

Medium Speed: 5,280 feet / second initial “landing” speed

Low Speed: 2,625 feet / second initial “landing” speed

For general comparison, the speed of a gun-bullet is about 2,500 feet / second.

“Runway” lengths (Limiting the list here for low-G only, for passengers):

High Speed Low G: “t” = 85.00 s, “d” 349,053 feet or 66.1 miles

Med Speed Low G: “t” = 54.65 s, “d” 144,276 feet or 27.3 miles

Low Speed Low G: “t” = 27.17 s, “d” 35,661 feet or 6.75 miles

On Earth, the longest paved runway (see https://www.telegraph.co.uk/travel/lists/shortest-airport-runways/and-the-longest-runway-/?wgu=275405_73669_15771129382853_16db357afd&wgexpiry=1584888938&WT.mc_id=tmgoff_paff-30828_subsoffers_basic_planit_us&utm_source=tmgoff&utm_medium=tmgoff_paff-30828&utm_content=subsoffers_basic&utm_campaign=tmgoff_paff-30828_subsoffers_basic_planit_us ) is 18,045 feet… * 1 mile / 5,280 feet = 3.42 miles long… 66 miles of runway on the moon would be absurdly costly, and can be eliminated from our thinking (high speed here was defined as Apollo-style “free return” orbit from Earth to moon and back, w/o an “orbit insertion” burn at the moon). There is NO cheating the length of a decelerator at a given incoming speed and a given maximum “G” force! 66 miles is out of consideration!

The speed listed here as “medium” speed is a 69-mile-high Apollo-style orbit, which is sensible for an incoming craft that will often be multi-purposed… Releasing small-sats, robot landers, and cargo vessels, for example. The lower orbit is also sensible for tourists, who will want to loiter and sight-see (during a few moon orbits, before landing). The “runway length” (27.3 miles ) is still prohibitive, but it might not have to be TOTALLY prohibitive. The slowest listed incoming speed wouldn’t save us much fuel (reaction mass), so let’s stop looking at that slowest speed, and focus on the middle speed.

A 27.3 miles-long runway sounds very scary, so what can we do? The mooncrete-lined “runways” described so far might be compared to concrete highways on Earth, costs-wise. Per-mile costs of a modern concrete highway:

https://blog.midwestind.com/cost-of-building-road/ says: “…for the production of a 4-lane highway, the cost per mile will run between $4 and $6 million in rural or suburban areas…”

Now on the other hand, consider per-mile costs of high-tension transmission lines: https://www.power-grid.com/2013/02/01/underground-vs-overhead-power-line-installation-cost-comparison/#gref says… “A new 138 kV overhead line costs approximately $390,000 per mile…”

So QUITE clearly, we could save LARGE amounts of money, by putting significant fractions of the length of our “runway” up above the surface of the moon, suspended by wires or cables, on towers. So this is one of the ideas that will be discussed in greater detail, below.

Another set of options to be explored below, could be illuminated by some analogies. Target practice aficionados (whether shooting bullets or arrows) know that a layer or two of straw bales behind their paper bull’s-eye target will stop their bullet, or stop their arrow. You can even fish the bullet out of its path through the straw (retrieve the bullet) if you want to. But that’s a lot of concentrated-in-time “G” force on your imaginary little homunculus riding along on the inside of your bullet! To take it MUCH easier on your imaginary homunculus, you might want to take your 4 or 5 feet of straw bales’ thickness, and shoot, instead, through 100 layers of cardboard (or cloth, paper, etc.), with each layer of cardboard being separated from the next, by 10 yards or so. Your imaginary homunculus now gets a bit of a rough ride, from jack-hammer-like stacked-shocks vibrations, but your homunculus doesn’t get turned into a flattened jellyfish of squashed protoplasm. We could do a similar type of thing with our passenger-containing moon-landing bullet.

We have already discussed slowing down our vessel with clouds of moon dust, and we have already discussed “break sticks”, or more complex restraining devices. In our bullet-stopping analogy, the layer upon spaced layer of cardboard simply becomes layer upon spaced layer of much-larger areas of some sort of sacrificial material to be broken through. These materials are arrayed in free space (up on pedestals or on suspended cables) instead of in a trough. Instead of sticks, they are circles, squares, rectangles, or some other shape with enough area to encompass the entire cross-sectional area of our passenger-craft bullet shape (only the bullet shape will be discussed in this context).

When we were discussing sacrificial high-G cargo craft, we didn’t care much about the outer surfaces of the vessel getting abraded away. Things change, and they change a LOT, now that we are targeting passenger vessels! Abrasion or erosion needs to be strictly avoided! Also, we have a problem with trying to control our vessel’s path (and attitude) as it “swims through” dust clouds and-or impeding layers of “cardboard targets”, to coin a short-hand term here. As we “swim through” these things, it would be nice if our bullet was shaped at least vaguely like a fish, to guide our course and attitude!

This can be done at the nose of the craft, by adding a spear-point, like a narwhal’s tusk, or the nose of a swordfish. The spear is followed by a shallow-curved dome, expanding in size as the distance from the spear-point increases. This is followed by a metal skirt, like the metal skirt on a steamer basket or metal colander with folding metal leaves (see https://www.bedbathandbeyond.com/store/product/zyliss-reg-stainless-steel-11-inch-steamer-basket/1010164354?skuId=10164354&&mrkgcl=609&mrkgadid=3253336594&enginename=google&mcid=PS_googlepla_nonbrand_kitchenfoodprep_local&product_id=10164354&adtype=pla&product_channel=local&adpos=1o2&creative=356249224553&device=c&matchtype=&network=g&gclid=Cj0KCQiAl5zwBRCTARIsAIrukdMgCnxUnGAqZGi1VXgkcneq8H18UBtk9fNVSMy0VQTl4B2K30_n6_MaAiBPEALw_wcB&gclsrc=aw.ds for a sample image).

This (above-described) arrangement can be moved (and firmly held in a desired position) by actuators of any suitable type, with hydraulic actuators being your best bet, with current technology. Up-and-down motions are enough, for now (actuated ball-and-socket joints are possible, and provide more freedom of movement, but are judged to be too complex, costly, and high-maintenance, for this application). Up-and-down motion only is enough, perhaps, but it would be HIGHLY desired, if the metal skirt (for providing motion and protection at the same time) of this first stage is immediately followed by another, similar stage (again with the metal skirt) that is actuated around a rotational axis that is perpendicular to the first axis. That is, add the ability to swing your nose-spear-tip left and right, to your ability to swing it up and down. Now, our “swimming fish” can point its nose as is desired, to assist in course and attitude control.

The above MIGHT be enough. If not, at the aft end of the craft, we could add (quantity 6 might be optimal) fins that normally hug the rear of the craft. When needed, however, they can differentially be swung out (on one side but not another) by actuators, to catch more dust (or “cardboard targets”) to add additional course and attitude control. OR, they can ALL be puffed further out, to slow down, or pulled in, to speed up. For a visual analogy of these rear fins swinging out, think of a scared fish or reptile puffing out (swinging out) the free ends of its scales, to make itself appear larger and scarier to an opponent.

All of this brings up a very important issue: HOW do we prevent abrasion? After all, moon dust is highly abrasive. And whatever our “cardboard targets” might be made of (however soft they might be) doesn’t matter much, if we are (as we must, for this whole scheme to be worthwhile) hitting the moon dust and the “cardboard targets” at bullet speeds and higher. It would be nice if we had “super materials” to use, to build our (“Star Trek” evoking) “deflector shields”! That is, for all of the outermost surfaces of our front spear, dome-shield, and metal skirts, and for the rear deflector fins.

As it turns out, “super materials” (both extremely hard and impact-resistant) are a real thing! The reader is left to do their own internet research (there’s plenty of reading material out there) concerning this, but note, your best search-strings are “glassy metals” and “amorphous metals”. A very short summary is as follows: With current technologies, some of the VERY best glassy metals are made of a wild variety of different atomic sizes of many different types of metal elements. The wild riot of different sizes of atoms prevents the normal formation of jumbled small crystals of metal, as is the case with most metals and alloys. The requirement for a wild variety of atom sizes, though, dictates that we MUST include VERY expensive precious elements such as gold and platinum (for top-quality metallic glass). That places the best glassy metals out of reach for many potential users. Top-quality glassy-metal tank armor for armies would work rather well, but would bankrupt any user today. An interesting link here (related to both glassy metals and space travel) is https://www.scmp.com/tech/science-research/article/1850863/metallic-glass-stronger-titanium-could-be-used-build-next .

By the time moon colonies have refined the “hard landings” techniques described here (or similar), for cargo vessels, AND they’re ready to try the use of similar technologies for passenger vessels, the mining of asteroids may quite likely be well underway. The likes of gold and platinum may become readily available in affordable, higher bulk quantities, and our glassy-metal “deflector shields” might become practical. So let’s proceed with more fending off of the future patent trolls!

Now I trust that before we move on, the above text for describing “fishy” attributes of our “swimming” bullet-vessel are enough. Readers desiring illustrations may email me at RocketSlinger@SBCGlobal.net . I’ve not bothered to add the needed drawings clutter to add those, to bullet drawings below.

Parenthetically, I would add, please don’t ask me for the gory details about which exact attitudes of the “fish-bullet” are desired, for which kinds of attitude and course changes! I’m trained as an electrical engineer, not a physicist. Intuitively, I believe that the nose should be adjusted to point towards where we want to go towards. I also believe that the rear fins should be deployed pointing towards the side that we want to be pointed towards (up, down, sideways). This is on the theory that the body will be hind-end-spun away from the side that we “deflect matter” towards… The matter-pushing vector will rotate us around the center of mass, to accomplish this. The spinning-around-the-center-of-mass idea applies to actions taken at both fore and aft ends of the vessel, actually. “Elements analysis” and aerodynamics (dustodynamics for flying through dust clouds?) would be needed to flesh this out, in more detail. Don’t ask me!

The only other thing that I can add, with some confidence, is that one might best plan to half-deploy ALL of the rear fins, in a balanced manner, as the default plan. If we are BEHIND our planned course, and want to go faster, we retract ALL of the fins. Conversely, if we are AHEAD of our planned course (travelling too fast), we more-fully deploy ALL of the fins, in a balanced manner, to slow down, aircraft “flaps” or “spoiler” style.

Interlude follows for boring details and math… For linear-style readers who like to read straight on through, from start to finish, and ESPECIALLY for readers who don’t mind boring details and math, please read straight on through. For those who want to skip such things, please search for (or go to) “I skipped the boring details and some math”.

Do we need to consider the curvature of the moon’s roughly spherical shape, when designing our “runway”? The answer is “no”, but let’s take a quick look at the math. The moon’s circumference is generally accepted at 6,786 miles. Our targeted decelerator (“runway”) length is 27.3 miles, at medium speed and low “G”. 27.3 miles then is 27.3 / 6,786 miles = 0.4 %, 0.4 % * 360 degrees = 1.4 degrees out of 360 degrees dropped over 27.3 miles… This can be safely ignored. Done!

A 27.3 -miles-long runway won’t be built cheaply! So we MUST cut costs wherever it can be done safely! Parts of it are just dust clouds, parts of it are strung up on cables, and so forth. To allow us to get a better intuitive feel for what might be optimal, a table of speed-v/s-distance-along-the-“runway”, all assuming pulling 3 Gs all along, would be very handy. Let’s build the table. 0 (zero) miles and starting-speed of 5,280 feet / sec is the start, 27.3 miles and zero speed is the finish. A gun-bullet-speed of 2,500 feet / sec makes a handy reference point.

Deriving a speed at (for example) 1-mile increments along the 27.3 miles is rather painful mathematically. It is easier to take the below math results (repeated from far above) and work in time-increments from there.

Medium Speed Low G: “t” = 5,280 feet / second * 0.01035 sec² / ft

= 54.65 seconds (Added comment: 0.01035 sec² / ft = 96.6 ft / sec²)

So let’s start at 0 seconds and add 5 seconds at each step, to get to 55 seconds.

0 (zero) seconds, speed is 5,280 feet / sec.

In 5 seconds we decelerate by (96.6 figure is derived far above) 96.6 ft / sec² * 5 sec = 483 ft / sec, so our current speed is 5,280 ft / sec minus 483 ft / sec = 4,797 ft / sec.

5 seconds after that (total 10 seconds), we are starting this next 5-second increment of deceleration at a starting speed of 4,797 ft / sec (from above), so we do the math again, and it is clear that we drop another 483 ft / sec for every new 5 seconds of time expired. So then…

0 (zero) secs, 5,280 feet / sec.

5 secs, 4,797 ft / sec.

10 secs, 4,314 ft / sec.

15 secs, 3,831 ft / sec.

20 secs, 3,348 ft / sec.

25 secs, 2,865 ft / sec.

Gun-bullet-speed of 2,500 feet / sec reference point.

30 secs, 2,382 ft / sec.

35 secs, 1,899 ft / sec.

40 secs, 1,416 ft / sec.

45 secs, 933 ft / sec.

50 secs, 450 ft / sec.

54.65 sec, 0.0 ft / sec (Assumed / interpolated).

55 secs, -33 ft / sec. (Rounding error; call it zero)

Now let’s recall from far above that Distance = t v _(mean).

So… Averages fall smack in the middle of start-speed and end-speed, basically… On odd-numbered entries, then, we can just use the middle entry from previous entries, for average speed… 5 secs is the ave-speed for 10 secs, 10 is the ave-speed for 20, etc.

Time Speed Distance

0 secs, 5,280 ft/ sec, 0 distance.

5 secs, 4,797 ft / sec, average speed = (5,280 + 4,797) / 2 ft / sec = 5,038.5 ft / sec for v _(mean) ; * 5 secs = 25,192.5 feet

10 secs, 4,314 ft / sec, 4,797 ft / sec * 10 secs = 47,970 feet

15 secs, 3,831 ft / sec, ave = (5,280 + 3,831) / 2 ft / sec = 4,555.5 ft / sec for v _(mean) ; * 15 secs = 68,333 feet

20 secs, 3,348 ft / sec, 4,314 ft / sec * 20 secs = 86,280 feet

25 secs, 2,865 ft / sec, ave = (5,280 + 2,865) / 2 ft / sec = 4,072.5 ft / sec for v _(mean) ; * 25 secs = 101,813 feet

Gun-bullet-speed of 2,500 feet / sec reference point.

30 secs, 2,382 ft / sec, 3,831 ft / sec * 30 secs = 114,930 feet

35 secs, 1,899 ft / sec, ave = (5,280 + 1,899) / 2 ft / sec = 3,589.5 ft / sec for v _{(mean) ;} * 35 secs = 125,633 feet

40 secs, 1,416 ft / sec, 3,348 ft / sec * 40 secs = 133,920 feet

45 secs, 933 ft / sec, ave = (5,280 + 933) / 2 ft / sec = 3,106.5 ft / sec for v _{(mean) ;} * 45 secs = 139,793 feet

50 secs, 450 ft / sec, 2,865 ft / sec * 50 secs = 143,250 feet

54.65 sec, 0.0 ft / sec, ave = (5,280 + 0) / 2 ft / sec = 2,640 ft / sec for v _(mean) ; * 54.65 secs = 144,276 feet

Now repeat the above table for time-speed-distance, with the calculations clutter cut out…

Time Speed Distance

0 secs, 5,280 ft/ sec, 0 distance.

5 secs, 4,797 ft / sec, 25,192.5 feet

10 secs, 4,314 ft / sec, 47,970 feet

15 secs, 3,831 ft / sec, 68,333 feet

20 secs, 3,348 ft / sec, 86,280 feet

25 secs, 2,865 ft / sec, 101,813 feet

Gun-bullet-speed of 2,500 feet / sec reference point.

30 secs, 2,382 ft / sec, 114,930 feet

35 secs, 1,899 ft / sec, 125,633 feet

40 secs, 1,416 ft / sec, 133,920 feet

45 secs, 933 ft / sec, 139,793 feet

50 secs, 450 ft / sec, 143,250 feet

54.65 sec, 0.0 ft / sec, 144,276 feet

Now repeat the above table, adding miles (5,280 ft/mile)

Time Speed Distance

0 s, 5,280 ft/s, 0 distance, 0 ft, 0 miles.

5 s, 4,797 ft/s, 25,192.5 ft, 4.77 miles

10 s, 4,314 ft/s, 47,970 feet, 9.09 miles

15 s, 3,831 ft/s, 68,333 feet, 12.9 miles

20 s, 3,348 ft/s, 86,280 feet, 16.3 miles

25 s, 2,865 ft/s, 101,813 ft, 19.3 miles

Gun-bullet-speed of 2,500 ft/s reference point.

30 s, 2,382 ft/s, 114,930 feet, 21.8 miles

35 s, 1,899 ft/s, 125,633 feet, 23.8 miles

40 s, 1,416 ft/s, 133,920 feet, 25.4 miles

45 s, 933 ft/s, 139,793 feet, 26.5 miles

50 s, 450 ft/s, 143,250 feet, 27.1 miles

54.65 s, 00 ft/s, 144,276 feet, 27.3 miles

So our total “runway” length is 27.3 miles, with the vast majority of it being at high speed, and a small part at the end, being at slow speeds. Let’s just do a little bit more “boring math” before we start looking at some (at least tentative) engineering conclusions.

What sort of drop (due to the moon’s gravity) might we be looking at, during these approximately 55 seconds? Now, recall that our design will call for a “fish-bullet”, which can “swim” by changing its shape (point its nose, and deploy radially-arranged, outward-pointing spoilers on its rear). So, by deflecting material (dust in dust clouds, and speed-impeding layers of “cardboard targets”, etc.) downwards, creating an upwards vector, we can constantly counteract the moon’s weak gravity. Our flight path can deviate from being totally straight, and be some sort of (at least mildly curved) upward or downwards or sideways curved path, at our desire, and under our control. We should at least do SOME amount of math, and build SOME sort of minimal table, though, to give us an informed grasp of “what our fish-bullet wants to do”, ignoring our interference (path deflections).

The moon’s gravity is 0.1654 “G” = 5.33 ft / sec² … Assume that we start (as determined by previous rocket and cold-gas-thrusters blasts; AKA orbital maneuvers) with zero velocity upwards or downwards with respect to the moon’s surface. Distance is average-speed (half-speed in this case) times “time” as usual.

Time . . . . . . . . . . . . . . . Speed . . . Distance

‘0 . . . . . . . . . . . . . . . . . 0 ft/s . . . 0.00 ft

‘1 s … 1 s * 5.33 ft/sec2 = 5.33 ft/s 2.67 ft

‘2 s … 2 s * 5.33 ft/ sec2 = 10.66 ft/s 10.7 ft

‘3 s … 3 s * 5.33 ft/sec2 = 16.0 ft/s 24.0 ft

‘4 s … 4 s * 5.33 ft/sec² = 21.3 ft/s 43.0 ft

‘5 s … 5 s * 5.33 ft/sec² = 26.65 ft/s 66.6 ft

… (take bigger time-steps here on in) …

‘10 s … 10 s * 5.33 ft/sec² = 53.3 ft/s 267 ft

‘15 s … 15 s * 5.33 ft/sec² = 80.0 ft/s 600 ft

‘20 s … 20 s * 5.33 ft/sec² = 107 ft/s 1,070 ft

‘25 s … 25 s * 5.33 ft/sec² = 133 ft/s 1,663 ft

‘30 s … 30 s * 5.33 ft/sec² = 160 ft/s 2,400 ft

‘35 s … 35 s * 5.33 ft/sec² = 187 ft/s 3,273 ft

‘40 s … 40 s * 5.33 ft/sec² = 213 ft/s 4,260 ft

‘45 s … 45 s * 5.33 ft/sec² = 240 ft/s 5,400 ft

‘50 s … 50 s * 5.33 ft/sec² = 267 ft/s 6,675 ft

‘55 s … 55 s * 5.33 ft/sec² = 293 ft/s 8,058 ft

In conclusion (from the above), the downward vector from the moon’s gravity (in any schemes of dust clouds, “cardboard targets”, etc., for parts of a “runway”) must be nearly-constantly corrected. Every 1 to 3 seconds or so (at least until the vessel makes some sort of solid contact with the moon’s surface, or extensions of the moon’s surface), we’d better take that downward speed and “nip it in the bud”, before it builds up too much! Let’s wait (till further below) to reach more engineering conclusions.

Now as a bit of mostly-gratuitous math (as a refresher course, too), let’s see how we would go about (with or without looking at the above table) figuring out “exactly how long would it take us to drop 400 feet in the moon’s gravity”? We COULD use interpolation to get an APPROXIMATE answer, perhaps (I tried it, and it was messy and results were significantly wrong), but that would require building the table first, anyway. Let’s see how we would do it “from scratch”.

Distance = t v _(mean) = t * initial velocity / 2

What is our velocity by the time that we have dropped 400 feet?

after 1 sec, “V” ft / sec = 1 sec * g ft / sec²
after 2 sec, “V” ft / sec = 2 sec * g ft / sec²
after 3 sec, “V” ft / sec = 3 sec * g ft / sec²

after “X” sec, “V” ft / sec = X sec * g ft / sec² , so…

Just do it iteratively again…

after 1 sec, 5.33 ft / sec² * 1 sec = 5.33 ft/sec; “d” = 1 sec * ( 5.33 ft/sec / 2) = 2.665 feet

after 2 secs, 5.33 ft / sec² * 2 sec = 10.66 ft/sec; “d” = 2 sec * ( 10.66 ft/sec / 2) = 10.66 feet

after 3 secs, 5.33 ft / sec² * 3 sec = 15.99 ft/sec; “d” = 3 sec * ( 15.99 ft/sec / 2) = 23.99 feet

…

Generalizing for this exact scenario,

after X secs, Velocity = 5.33 ft / sec² * X sec = ( 5.33 * X ) ft/sec; “d” = “400 feet” = X sec * (( 5.33 * X ) ft/sec / 2) = 400 feet

400 feet = (X² feet * 5.33 / 2)

800 feet = (X² feet * 5.33)

800 / 5.33 feet = X² feet

150 feet = X² feet

X = square-root of 150 = 12.3 seconds

Double-check this for sanity!

after 12.3 secs, 5.33 ft / sec² * 12.3 sec = 65.6 ft/sec; “d” = 12.3 sec * ( 65.6 ft/sec / 2) = 400 feet; check!

Now it is time to dispense with the math, and return to engineering ideas.

“I skipped the boring details and some math”

“I skipped the boring details and some math” search-string is here… Start in from here on down again, please!

If we’ll examine the above result summaries, keeping in mind the benchmark comparison to a gun-bullet speed… And just HOW MUCH damage the kinetic energy of a bullet does, upon impact… We might want to think about using dust clouds (or clouds of dust mixed with some other travel-impeding matter) for long enough to cut our speed down to about half of the speed of a bullet, before we make ANY kind of contact with moon-surface-mounted deceleration devices. So that knocks about 25 miles off of the length of our “runway” here.

We have already discussed dust-clouds enough, both here, and surrounding Figure #1 at http://www.rocketslinger.com/Ping_Pong_ME/ , so that little remains to be said concerning that. Enough “defensive publishing” (concerning that) has probably been done already. So, the few following comments are (mostly) merely for the sake of “complete coverage”.

The further away our moon-dust-launchers are, from the vessel’s path, the more that the “throw cones” (of dust) will start to lose focus on the path of the vessel (the less efficient that the thrown-dust scheme becomes). On the other hand, if the dust-throwers get TOO close to the intended path, we risk collisions! So we have to find a balance. And clearly, a high premium is thrown onto the desirability of a precisely controlled flight path. Dust-throwers could be located up on top of suspended wires (cables), for optimal placement, regardless of deviations in the terrain (moon-ain? Lunain?) below the cables. That should be kept in mind, as we discuss tower-cables and cable-mounted decelerator devices further below.

Frictional heat build-up (just like on a heat shield of a spacecraft re-entering the Earth’s atmosphere) will be a problem, as we fly our vessel through dust clouds. SpaceX briefly toyed with “transpiration cooling” for cooling a spacecraft’s skin, during re-entry. More design ideas associated with this particular idea are detailed at http://www.rocketslinger.com/Psv_Tgt_Fsw/ (the same document can also be found at https://www.researchgate.net/publication/331556573_Designs_for_Passively_Thermally_Gated_Fluid_Flow_Switches ), and these ideas could be used here, when slowing down by slamming through dust clouds. The ideas there might need to be modified for the use, here, of glassy metals instead of stainless steel, there. For melting points of glassy metals, after a cursory internet search, I find very little. A high melting point does NOT seem to be a commonly cited benefit of glassy metals! One’s best approach may be to take SpaceX’s “stainless steel sand which” approach, add PLENTY of transpiration cooling (again, see http://www.rocketslinger.com/Psv_Tgt_Fsw/ ), and then add a layer on the outside of the stainless steel, of glassy metal for mechanical resistance to abrasion. One would have to over-cool the underlying layers to protect the (outermost layer of) glassy metals from melting. The required amount of cooling fluid (liquid nitrogen perhaps?) might be too large for this whole idea to be practical. Analysis is clearly needed on that point!

Getting back to over-all design engineering here, I do not know (nor do I know how to calculate) how much dust (or other impeding matter) we’d have to throw up, into the path of our vessel, to provide a fairly steady 3 G of deceleration over a stretch of 25 miles (see above), so as to decelerate our craft to low-enough speeds, that it could safely start making more-solid contact with moon-surface-mounted decelerator devices. Frankly, now that the calculations are done, I doubt that this whole scheme can be made practical (economical) for passenger craft. The further-above ideas concerning high-G (semi-sacrificial) cargo craft remain quite attractive, for practicality, in my opinion. Low-G passenger craft do not! That is, not as anything near a “total solution”, certainly. We could kill SOME speed using dust clouds, and then land conventionally, under rocket power, as a step towards saving SOME rocket fuel.

Still, let us continue. Some of the below ideas and drawings will possibly help better document (flesh out) cargo-craft-related design ideas. The more ideas (no matter how implausible today) that we describe, and the more details that we provide (within reason), the more that we can fend off tomorrow’s patent trolls! And enable future, affordable space travel! So let’s continue!

Tower-top-mounted high-tension cables can be mounted on the moon, with decelerator devices mounted on the wires. With the moon’s weak gravity, lack of winds, storms, strong earthquakes, etc., tower-building will be, in some ways, easier than on Earth. Temperature extremes are worse, though, and, of course, human workers need a LOT more protection! But it could be done!

The moon’s real estate costs (clutter of surrounding, expensive real estate that needs to be bought out for siting construction work) is way-way low, and will remain that way for quite a while! So we can be as generous as we want to be, in putting up many-many “guy wires”, to give us strength, without having to over-do on the towers. Guy wires will be needed to countervail against the weights that we want to suspend, and against stresses (forces) exerted on these suspended decelerator devices, as vessels pass through.

The below drawing assumes TWO lines of towers, suspending two parallel main cables. In between these cables, there are cross-cables. The middles of the cross-cables will be routed through rigid pipes (or some other hollow, solid, long element). Rigid pipes will stay fairly level, so long as the suspended cross-cable is properly adjusted (located in the sagging middle of the cable, with the cable-ends both located at the same vertical elevation). Any of many different types of decelerator devices can now be located on top of these pipes. Note that in the top-down view for the drawing below, the main cables will sag downwards in between towers, due to gravity pulling these cables down. This vertical sag isn’t visible to us in our top-down view. What IS visible to us, is inward sag (each side-cable towards the other) caused by the weights of the cross-cables, with their pipes that bear the weight of the decelerator devices.

The drawing assumes that the vessel travels from left to right, as it is slowed down. If (as will usually be the case here) deceleration is “lumpy” (non-linear, in short impulse-shocks, one impulse per each decelerator device), then we will want to space our decelerators fairly evenly (assuming that they are fairly evenly matched in the magnitudes of the impulses that they impart), but NOT over distance! We will want to space them evenly in TIME, instead, for a more-uniform average deceleration rate! So to the left (fast vessel travel), they are more widely spaced than to the right (slow).

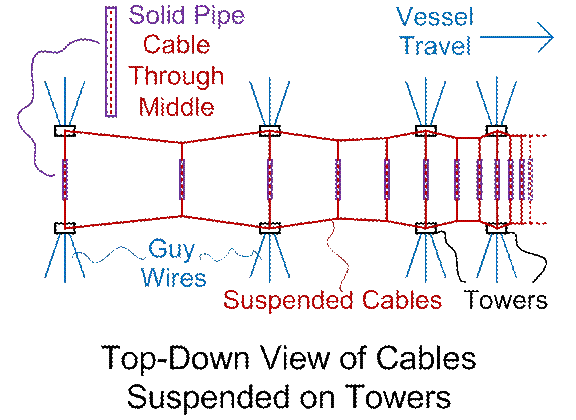
Figure #10

The cross-cables (shown routed through pipes color-coded as purple) are tightened the most (to a highest tension) when they are closest to the middle, between two towers. As these are located closer and closer to a tower, these cross-cables should be more and more slack-tensioned. This will compensate for the vertical “gravity slack” (between-towers droop) in the main cables from tower to tower. With abilities left in the system, to fine-tune the cross-cables tensions settings, the pipes should be able to be arrayed so that they are very, very closely aligned to all be in a straight line (all at the same vertical height off of the moon’s surface, or at a fairly precisely controlled tilt, with or without any built-in, controlled or desired curvature rate, as we travel with the vessel). Middle-most cross-cables being most tightly strung, these will pull the main cables closest to each other, as is shown in the drawing above.

What is NOT shown in the above conceptual-only drawing (to reduce visual clutter), is that many design-types of cable-top-mounted deceleration devices would benefit from a mounting PLATFORM, instead of just a mounting pipe. In many cases, these devices will be mounted on a platform spanning TWO pipes, for better mounting stability. The drawing only shows ONE pipe per variably-spaced location, to reduce visual clutter.

One small detail about where the cross-cables meet the pipes: If the pipe simply ends, at an unmodified sudden termination (especially with sharp edges), then any rocking, swaying, or sliding motion (as induced, for example, by the passage of a being-slowed-down vessel) of the pipe with respect to the cable, then the sharp edge of the pipe will tend to fray (and eventually cut) the cable that passes through the pipe. The pipe, here, should be joined to an outward-flaring “bugle horn”, shall we call it? When there are TWO pipes, firmly fastened (disallowing pipe spin), the bottom of the “bugle horn” can be lopped off, to form what essentially could be called a pipe-v/s-cable, motion bearing. If the decelerator device calls for only ONE pipe, with the pipe free to spin, then the “bugle horn” should NOT be lopped off, but should surround the cable by 360 degrees.

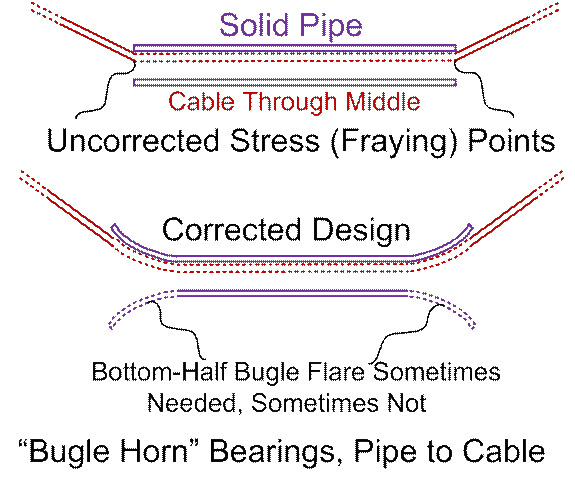
Figure #11

As previously briefly mentioned, the use of cables on towers will allow us to route parts of the “landing strip” up above raw, naked, un-improved terrain (or moon-ain, whatever you want to call it). Well, just like on Earth, a crude access road for towers-and-cables maintenance would be nice, but beyond that, the moon’s surface wouldn’t require much expensive modification. If optimal site selection (to include close proximity to where our settlement is located) allows it, we’ll want the flattest territory available. If not, some of the obstructing highest hills might need to have their tops knocked down. For SOME parts of the route, with any luck at all, we could skip the towers and cables, and mount the decelerating devices on low to medium-tall, solid pedestals.

I trust that none of the above deserves additional drawings. As usual, if more drawings are needed for clarification, please email me at RocketSlinger@SBCGlobal.net … The same applies as we continue below…

OK then… What all different kinds of decelerator devices might be mounted on cables? Moon-dust-throwers, sure, but those have already been thoroughly described.

Here’s another idea that I consider highly implausible (too expensive), but let’s just get it out of the way. How about electromagnetic mechanisms that mate (without physical contact) to other electromagnetic mechanisms in the vessel that’s being slowed down? “Levitating train” style? “Linear hysteresis brakes” style? AKA “eddy current brakes”? See https://www.globalspec.com/learnmore/motion_controls/clutches_brakes/linear_brakes for example. Also https://en.wikipedia.org/wiki/Eddy_current_brake . In my opinion, these would be too expensive and too heavy, to fill our needs. The gap (spacing) between the vessel, and the cable-mounted brakes, would need to be implausibly small, to be efficient, I think, as well.

How about a mostly-self-contained moon-dust-recycling fountain? Most of us are familiar with decorative water-recycling fountains, or even chocolate-syrup fountains. Do the same with moon dust (or other travel-impeding matter or mixture). A closely-co-located hopper-bin contains reserves of moon dust. The reserves will need topped off, as moon dust is lost to passing vessels. An uploader (Archimedes screw augur might be best, with the screw perhaps plated with glassy metals for erosion resistance) moves dust (when needed) up to the top of a “picture frame” (large rectangle), or to the top of a one-side-open, square-cornered “C” shape (think of a bar clamp). Another augur then moves the dust across the top-bar. Dust flows through gaps in the bottom of the top-bar. A flowing sheet of moon dust is thus presented to being-slowed-down passing-through vessels. A bottom “V” shaped trough, with another augur at the bottom, collects and recycles falling moon dust that is NOT blown off course by vessel traffic. Energize the augurs only when needed, of course. Done!

Yet another alternate idea: Take the “picture frame” as described immediately above, and fill the frame, not with a flowing sheet of moon dust, but, instead, with what we have previously called (shorthand from further above) a “cardboard target”. These targets could be made out of literal cardboard, sure, but that’s not a good material to be used on the moon. Plastics or other synthetics (that can be glued, or re-molten and reprinted using 3D printing), perhaps containing at least some moon dust, or thin-thin sheets of aluminum, or synthetics clad with thin aluminum for moon-weather (sun, heat and cold) resistance… Or thin plaster. These ideas sound more plausible. These “targets” may be more solid, or more fabric-like, as is practical. Robots (or other automation) can perhaps make repairs (or replacements) to the targets, between vessel passages, in an affordable fashion. Maybe!

One slight variation to the above would be a “double target”. Think of a belt sander. Two rolling cylinders (at least one of them powered) cycle the belt, round and round, as an option, but only if we want to make the belt large enough to accommodate several holes before needing a fresh patch job. Put a giant “belt sander” up there, allowing the vessel to pass through both layers. Outside of the vessel-passing-through areas of the belt, beef up the belt to make it stronger. Now we can take the belt down between passages of the vessels, for repair or replacement. This just MIGHT be a more affordable way to do things, in a highly implementation-details-dependent manner.

Somewhat slightly parenthetical comments follow: To whatever extent that these decelerator devices deliver discrete blows to the passing-through vessel… This would include ALL of the ones listed here, excluding only the blown-dust “dust cannons” and the electromagnetic (“hysteresis brakes”) methods… We must concern ourselves with HOW MANY of them we need. We have already remarked that they should be nearly evenly spaced out with respect to TIME OF PASSAGE, and not to linear-distance spacing. Using “logic by extremes”, we can imagine that one VERY SHARP blow to the vessel every 5 seconds endangers the vessel entirely too much, and that one blow per every 100 milli-S (one 10^th of a second) is entirely too expensive (too many decelerator devices). What is the balance here; what is the optimal frequency of impulse-blows? This is an important question!

I would speculate that 10 Hz (10 times per second) is on the low end. 20 Hz, perhaps, if we can afford it. From far above, we built a speed, time, and distance table, and concluded that (if we want to slow down to roughly half the speed of a gun-fired bullet, before making any sort of solid contact with moon-surface-mounted deceleration devices) we might want to suspend our deceleration devices up, for about 25 miles out of our 27.3 total miles. That is, roughly 40 seconds out of our total travel-time of 55 seconds.

Speculating further, perhaps for 20 of our first 55 seconds (for the first 16 miles), we could use “dust cannons”. Dust blown in this manner needs re-gathered and-or replaced, makes this rather painful, of course… That leaves another (yes, very speculative) 20 seconds of “impulse blows”. That’s 200 discrete decelerators at 10 Hz, and 400 of them at 20 Hz! So you can see ONE reason why I am skeptical about the whole idea here… But let’s march on…

The final category of discrete decelerator devices that I will now describe, do deserve some drawings. They were previously mentioned and called “guitar picks”, much further above (in the cargo vessels category). Each such discrete device could be mounted on ONE single suspended cross-pipe. The pipe would be left free to rotate (as a bearing), with it being biased into a preferred position by hanging-down weights (a pipe filled with moon sand, for example). Pointing upwards (tilted away from the oncoming vessel) would be our “guitar picks”, made out of stiff but flexible material, such as fiberglass, for example. The guitar pick’s vessel-contacting tips might best terminate into brush-bristles, to minimize damage to the hull of the passing, being-slowed-down vessel.

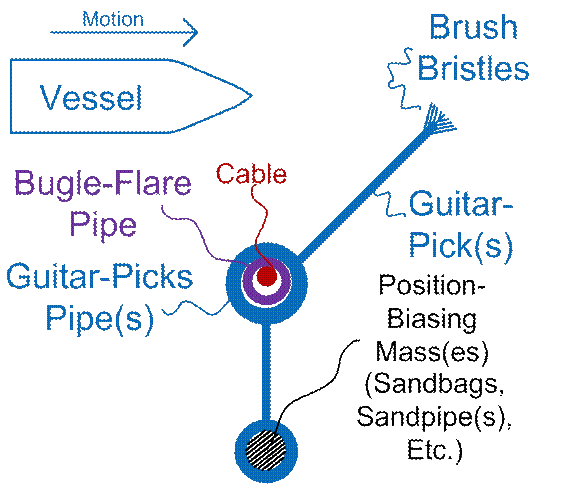
Figure #12

Note that above, one more outer pipe is added, so that there will be a motion-bearing between the inner and the outer pipe. This will cause less wear and tear on the cable. Some lubrication there would be nice, if one can be formulated to withstand the harsh environment. There will also then be less resistive force (including rotary inertia) keeping the “guitar pick” too-firmly in the path of the passing vessel. It does mean that the “bugle flares” at the inner-pipe ends (or, at least at one pipe-end per pipe) will need to be removed and replaced, every time that an outer pipe is replaced.

Note that so far, we have stipulated that the “guitar pick” method (with the bristles at the tips) might best be reserved for speeds well under the speed of a gun-bullet. Experimentally, we might want to slowly creep (this method) up towards higher speeds. But most of us have seen high-speed photos and slowed-down films of gun bullets doing their highly destructive “things”, so we have to remain very skeptical here, still. Constant repairs and replacements for high-speed-impacted “guitar picks” looks prohibitive. But what if some better “super materials” are invented in the future? Then the above (and continued below) ideas become far more viable, perhaps! If people can speculatively design “space elevators” using materials that don’t economically exist, yet, then we can do the same thing with giant guitar picks! Robotic repairs to guitar picks might also help to make these ideas more plausible. Perhaps we could even include methods of having feedstock materials and a 3-D printing mechanism at the bases of the “guitar picks”. The pick can now “grow” (self-heal its damage), just like a fingernail!

Next, here is a side view of such a guitar-pick. Note that it would likely be highly desired (for more-discrete, refined and rapid vessel-path-and-attitude adjustments) to break the “guitar pick” into multiple independent segments. I say that intuitively, without certainty, and I do NOT know how to do the physics or simulations! It is possible that the “spinning around the center of mass” problem, after the vessel is hit off-center, is worse than any benefit here, possibly. It is left as a mental-visual exercise to the reader, to alternately envision the “guitar pick” as being one solid piece, instead of as is shown below.

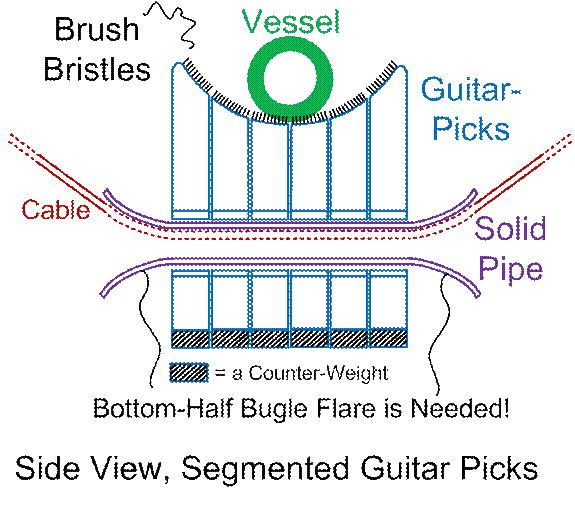
Figure #13

In addition to a bottom guitar pick (vitally essential for deceleration), it would be VERY highly beneficial to mount UPPER guitar picks as well. These may or may not need to be designed to touch the passing-through vessel frequently. If one wants frequent touching, locate them closer, of course. If one wants less-frequent touching, leave a bigger gap. If a large gap is left, then the upper guitar picks will serve ONLY as a safety measure, to quickly correct any vessel that starts to “snag” on the bottom guitar picks, causing the aft end of the vessel to start heels-over-head “tumbling” or “somersaulting”. If that starts to happen, the downward-pointing guitar picks will quickly correct the “tumbling” motion.

Since “lift balloons” won’t work on the moon, and pulley-operated gravity-inverting ropes or cables would be a mess, just about the only sensible option that we have left, to upward-bias the topside “guitar picks”, is to run another TWO sets of cables up top, as is shown below. Then use mechanical (or some other type of springs? Implausibly!) tension springs.

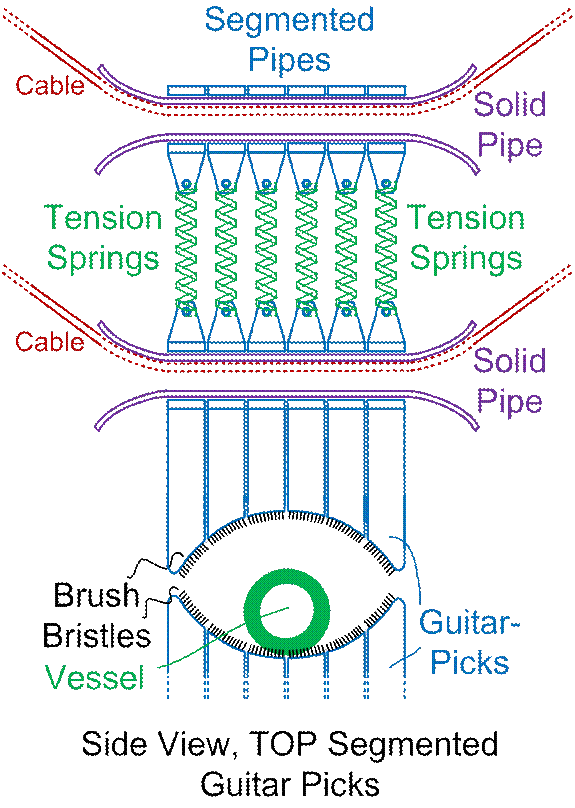
Figure #14

The above drawing is “conceptual only”…The vessel should be perhaps a wee tad larger, or the top guitar picks should be closer, for better guarding against “tumbling”, I suspect. The gap is (probably) shown being too large.

An end-on view of the above is easy enough to provide, and might provide more clarity, so here it is, below…

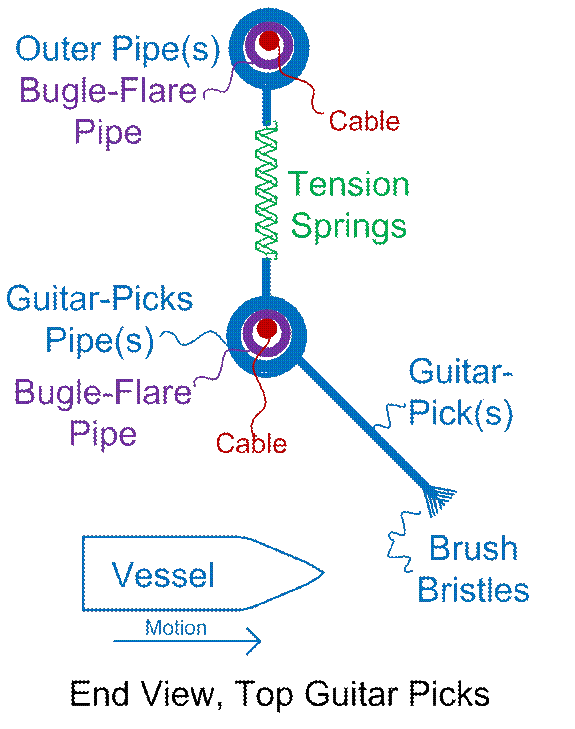
Figure #15

Summarizing some of the above, the bottom “guitar picks” are vitally essential, for keeping on “batting upwards”, the vessel, so as to counteract the moon’s gravity, as well as slowing down the vessel. The top-most “guitar picks” are perhaps SOMEWHAT less essential, but probably not much so. They are needed to near-immediately correct any “tumbling” problems.

At (probably) even less urgency, sideways “guitar picks” could be provided as well. Vertical cables, there, would replace horizontal cables… OR, towers could do the same jobs (as the vertical cables). Tension springs (not gravity and biasing masses) would again be used. All else would be highly similar to the two figures immediately above, except turned sideways. Side “guitar picks” would near-immediately correct “fish-tailing” errors, in the vessel travel path. If “guitar picks” are used on top, bottom, and both sides, what is shown above, for top and bottom, would need to shrink, of course, to make room. All this is left as mental and visual exercises for the reader.

What happens after the vessel is slowed down to a near-crawl, relatively? At the last few hundred feet of the “runway”? Well, it is possible (but not plausible) that the main side cables (see Figure #10; the side cables are where the cross-cables are mounted to, with the cross-cables mounting our deceleration devices) could be “beefed up”, towards the end, and a flat, solid road-bed (suspension bridge style) could be added here. To make this possible, the vessel would have to be equipped with landing gear (wheels). Wheels deeply embedded into the vessel, with only a bit of wheels protruding, permanently (not deployed only for “landing”), is not a plausible scheme, since horrible damage would be done to the wheels by any of the deceleration devices described above (with the exception of electromagnetic options, which are judged to be too expensive).

So… Could we deploy retractible (protected) landing gear rapidly enough, between the deceleration-devices phase of “landing”, and the REAL landing, on a roadbed? It is possible, but highly improbable, in my opinion. Wheels deployment speed here would have to be ridiculously fast. A proper term might be “laughable”, actually!

That leaves us one final, plausible ending for this scheme: At the final, slowest speeds, on could add an upward curve or deflection, to the “runway”, ski-jump style. The vessel is now sent at least slightly upwards, and the aft end swings below the fore end. The “ski jump” (up-ramp) would be nice, but isn’t absolutely needed. Perhaps 100 to 200 feet (or so) above the moon’s surface, though, the vessel DOES need to come off of the last deceleration devices, with SOME significant remaining speed… A few hundred feet per second, perhaps.

And now, the vessel can fire up its attitude-controlling jets or rockets (typically cold-gas jets), and its main aft rocket engines, to make a SpaceX-style (conventional) retropulsive landing. MUCH fuel would be saved by this whole scheme!

Once again, I believe that the high-G cargo delivery ideas are plausible, but the passenger-craft ideas are NOT plausible, with current materials and technologies. ALL of the ideas are included here for completeness, and for fending off the “patent trolls”!

I have no special expertise or any more plausible ideas concerning any associated matters here, so I will sign off at this time. This concludes my ideas as of this time. Once again, comments or questions (or idea contributions) are welcomed at RocketSlinger@SBCGlobal.net …

Stay tuned… Talk to me! RocketSlinger@SBCGlobal.net

Back to main site at www.rocketslinger.com